解题思路： ​

文名词规定如下：

1. 将 $101112 \cdots$ 中的每一位称为 数位 ，记为 $n$ ；
2. 将 $10, 11, 12, \cdots$ 称为 数字 ，记为 $num$ ；
3. 数字 $10$ 是一个两位数，称此数字的 位数 为 $2$ ，记为 $digit$ ；
4. 每 $digit$ 位数的起始数字（即：$1, 10, 100, \cdots$），记为 $start$ ；

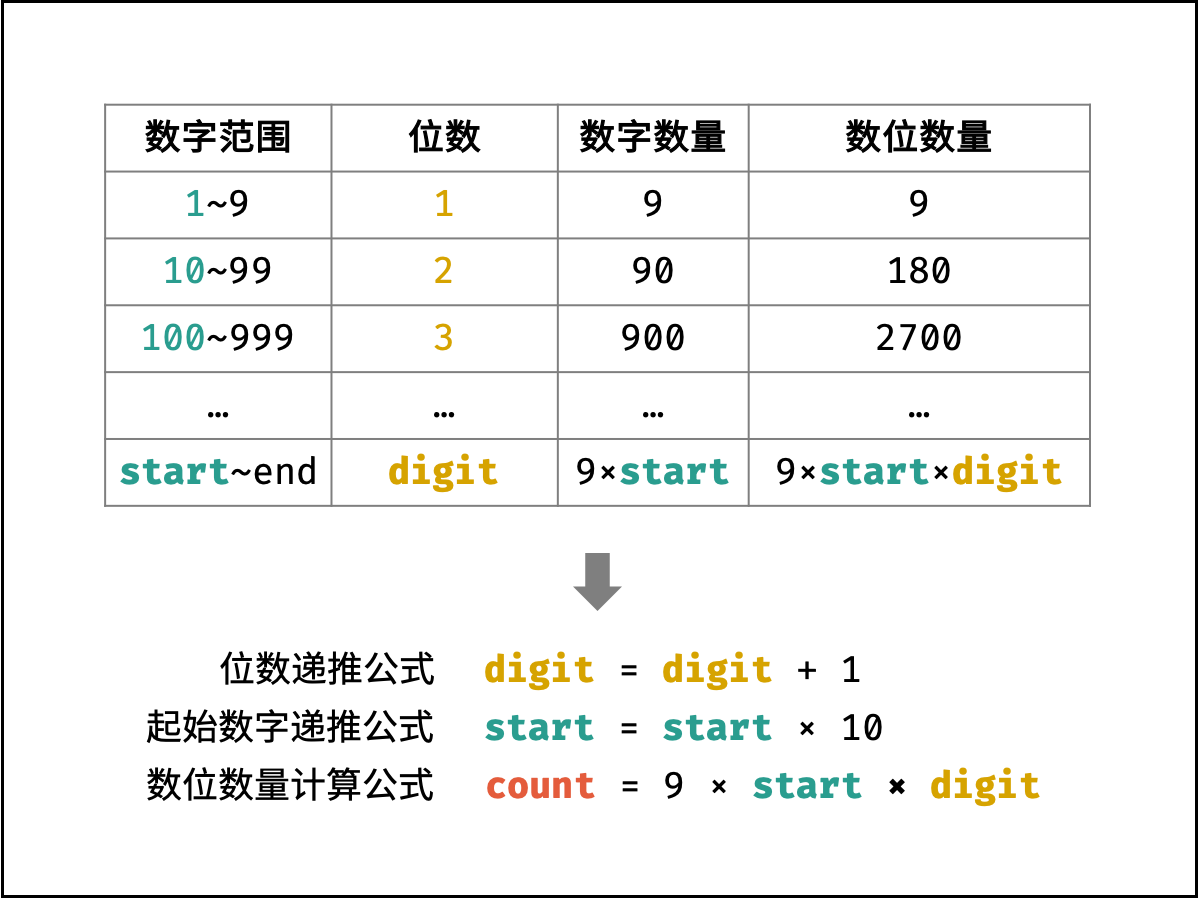
观察上表，可推出各 $digit$ 下的数位数量 $count$ 的计算公式：

$$ count = 9 \times start \times digit $$

根据以上分析，可将求解分为三步：

1. 确定 $n$ 所在 数字 的 位数 ，记为 $digit$ ；
2. 确定 $n$ 所在的 数字 ，记为 $num$ ；
3. 确定 $n$ 是 $num$ 中的哪一数位，并返回结果；

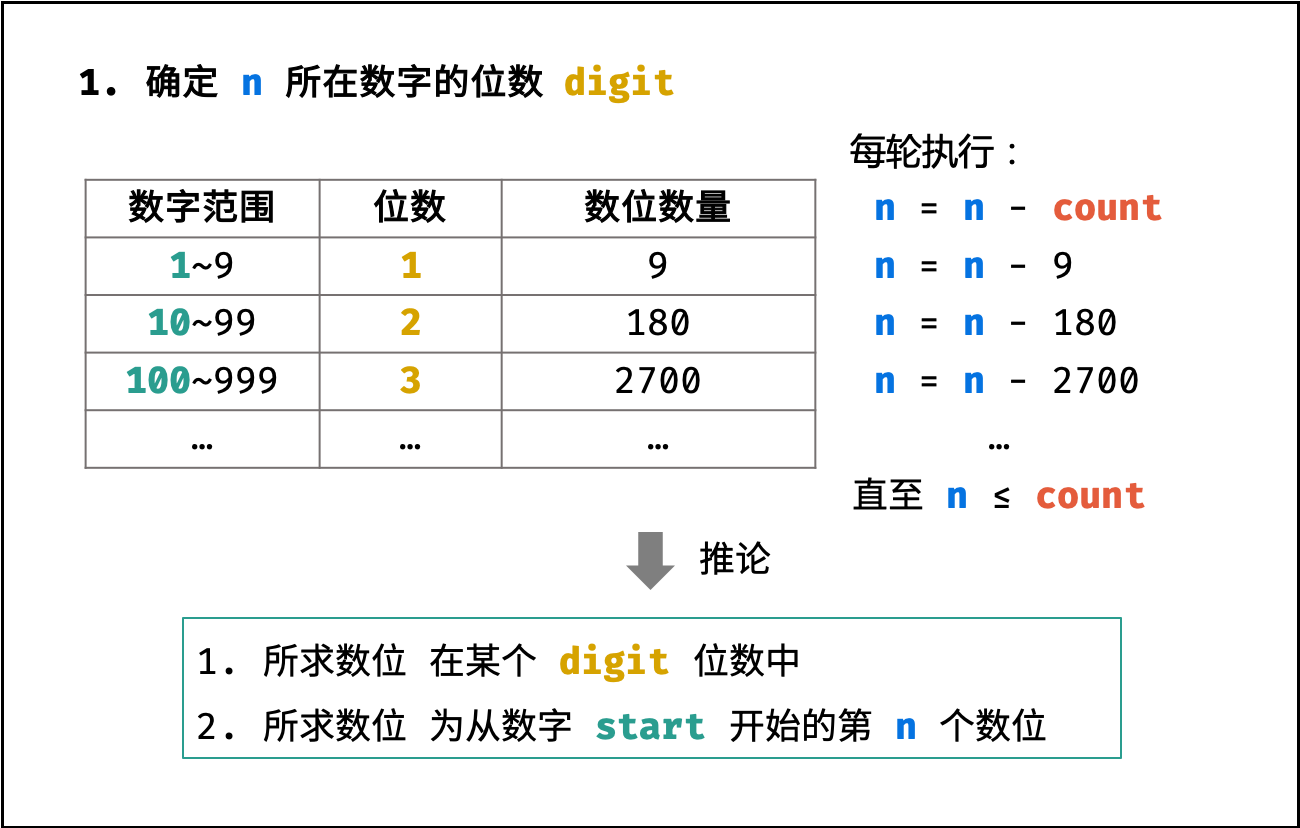
1. 确定所求数位的所在数字的位数 ​

如下图所示，循环执行 $n$ 减去 一位数、两位数、... 的数位数量 $count$ ，直至 $n \leq count$ 时跳出。

由于 $n$ 已经减去了一位数、两位数、...、$(digit-1)$ 位数的 数位数量 $count$ ，因而此时的 $n$ 是从起始数字 $start$ 开始计数的。

digit, start, count = 1, 1, 9
while n > count:
    n -= count
    start *= 10 # 1, 10, 100, ...
    digit += 1  # 1,  2,  3, ...
    count = 9 * start * digit # 9, 180, 2700, ...

int digit = 1;
long start = 1;
long count = 9;
while (n > count) {
   n -= count;
   start *= 10; // 1, 10, 100, ...
   digit += 1;  // 1,  2,  3, ...
   count = digit * start * 9; // 9, 180, 2700, ...
}

int digit = 1;
long start = 1;
long count = 9;
while (n > count) { // 1.
   n -= count;
   start *= 10; // 1, 10, 100, ...
   digit += 1;  // 1,  2,  3, ...
   count = digit * start * 9; // 9, 180, 2700, ...
}

结论： 所求数位 ① 在某个 $digit$ 位数中； ② 为从数字 $start$ 开始的第 $n$ 个数位。

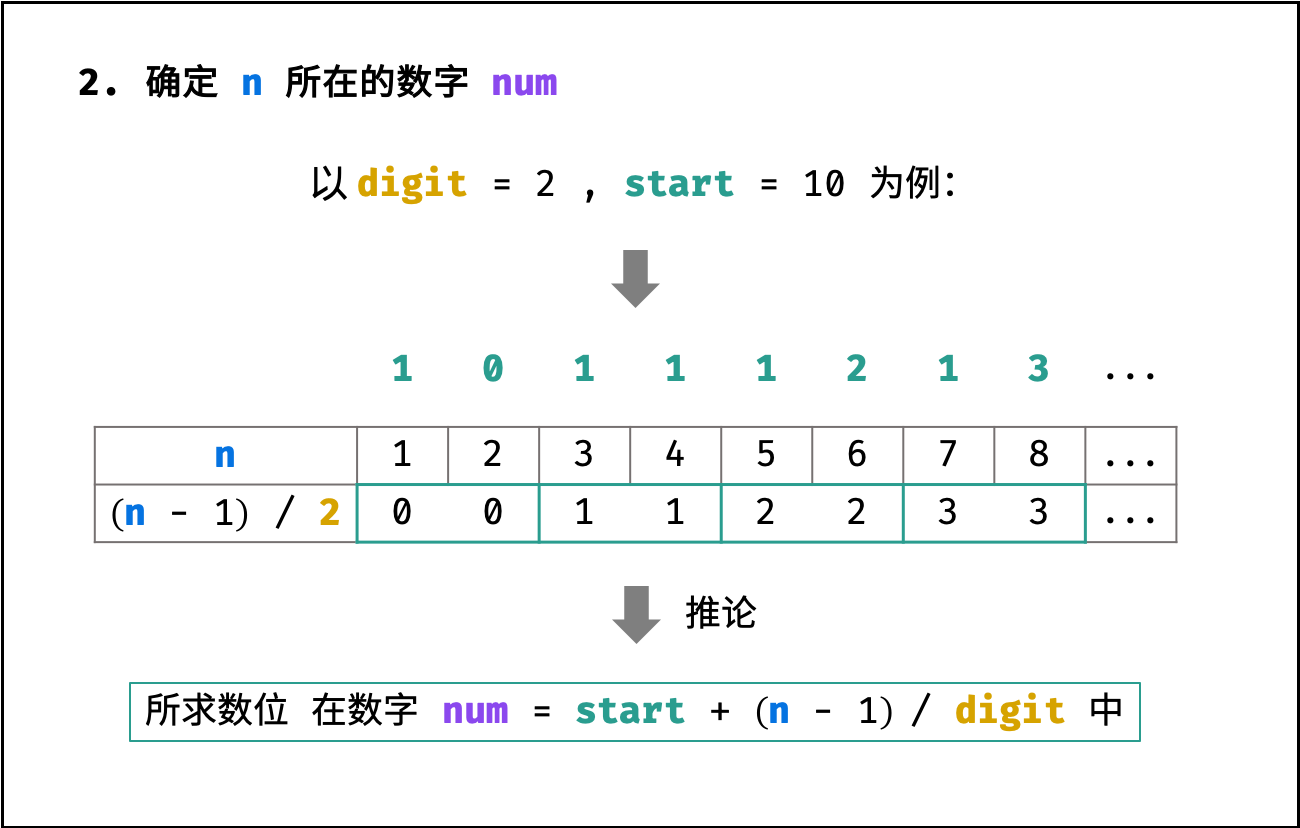
2. 确定所求数位所在的数字 ​

如下图所示，所求数位 在从数字 $start$ 开始的第 $[(n - 1) / digit]$ 个 数字 中（ $start$ 为第 0 个数字）。

num = start + (n - 1) // digit

long num = start + (n - 1) / digit;

long num = start + (n - 1) / digit;

结论： 所求数位在数字 $num$ 中。

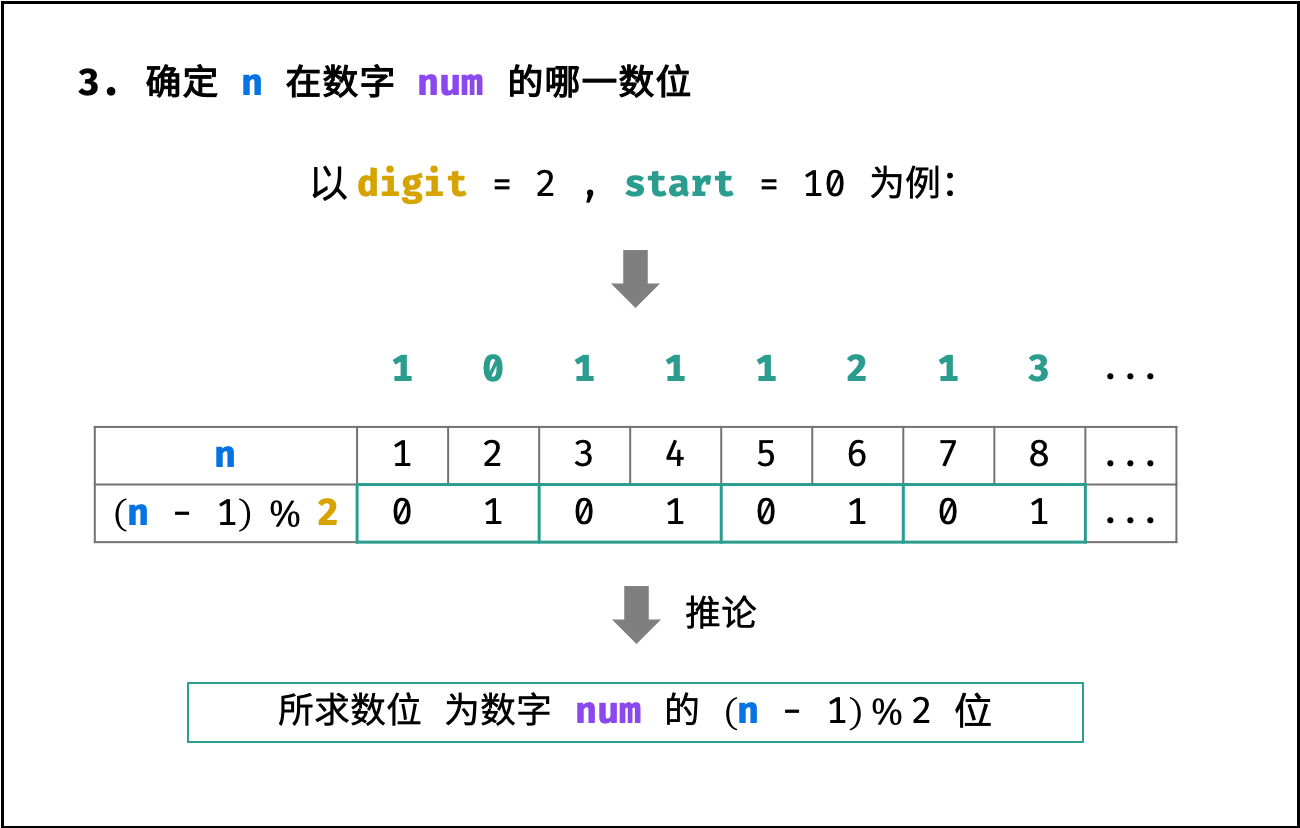
3. 确定所求数位在 $num$ 的哪一数位 ​

如下图所示，所求数位为数字 $num$ 的第 $(n - 1) % digit$ 位（ 数字的首个数位为第 0 位）。

s = str(num) # 转化为 string
res = int(s[(n - 1) % digit]) # 获得 num 的 第 (n - 1) % digit 个数位，并转化为 int

String s = Long.toString(num); // 转化为 string
int res = s.charAt((n - 1) % digit) - '0'; // 获得 num 的 第 (n - 1) % digit 个数位，并转化为 int

string s = to_string(num); // 转化为 string
int res = s[(n - 1) % digit] - '0'; // 获得 num 的 第 (n - 1) % digit 个数位，并转化为 int

结论： 所求数位是 $res$ 。

复杂度分析： ​

• 时间复杂度 $O(\log n)$ ： 所求数位 $n$ 对应数字 $num$ 的位数 $digit$ 最大为 $O(\log n)$ ；第一步最多循环 $O(\log n)$ 次；第三步中将 $num$ 转化为字符串使用 $O(\log n)$ 时间；因此总体为 $O(\log n)$ 。
• 空间复杂度 $O(\log n)$ ： 将数字 $num$ 转化为字符串 str(num) ，占用 $O(\log n)$ 的额外空间。

<,,>

代码： ​

class Solution:
    def findNthDigit(self, n: int) -> int:
        digit, start, count = 1, 1, 9
        while n > count: # 1.
            n -= count
            start *= 10
            digit += 1
            count = 9 * start * digit
        num = start + (n - 1) // digit # 2.
        return int(str(num)[(n - 1) % digit]) # 3.

class Solution {
    public int findNthDigit(int n) {
        int digit = 1;
        long start = 1;
        long count = 9;
        while (n > count) { // 1.
            n -= count;
            start *= 10;
            digit += 1;
            count = digit * start * 9;
        }
        long num = start + (n - 1) / digit; // 2.
        return Long.toString(num).charAt((n - 1) % digit) - '0'; // 3.
    }
}

class Solution {
public:
    int findNthDigit(int n) {
        int digit = 1;
        long start = 1;
        long count = 9;
        while (n > count) { // 1.
            n -= count;
            start *= 10;
            digit += 1;
            count = digit * start * 9;
        }
        long num = start + (n - 1) / digit; // 2.
        return to_string(num)[(n - 1) % digit] - '0'; // 3.
    }
};