自律小屋 | 自律小屋

解题思路：

若树 B 是树 A 的子结构，则子结构的根节点可能为树 A 的任意一个节点。因此，判断树 B 是否是树 A 的子结构，需完成以下两步工作：

先序遍历树 A 中的每个节点 $n_A$ ；（对应函数 isSubStructure(A, B)）
判断树 A 中 以 $n_A$ 为根节点的子树 是否包含树 B 。（对应函数 recur(A, B)）

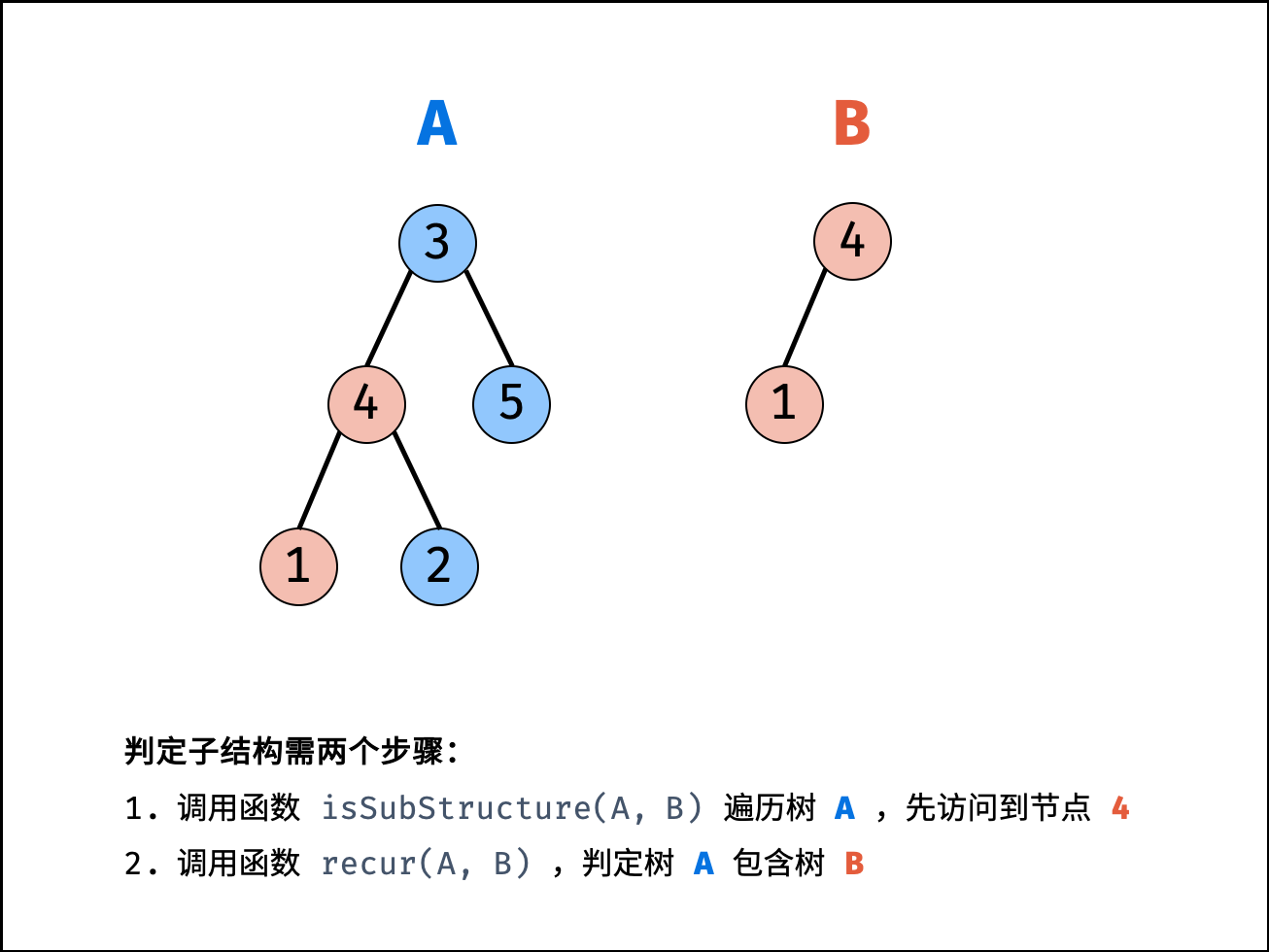
算法流程：

本文名词规定：树 A 的根节点记作 节点 A ，树 B 的根节点称为 节点 B 。

recur(A, B) 函数：

终止条件：
1. 当节点 B 为空：说明树 B 已匹配完成（越过叶子节点），因此返回 $true$ ；
2. 当节点 A 为空：说明已经越过树 A 的叶节点，即匹配失败，返回 $false$ ；
3. 当节点 A 和 B 的值不同：说明匹配失败，返回 $false$ ；
返回值：
1. 判断 A 和 B 的 左子节点 是否相等，即 recur(A.left, B.left) ；
2. 判断 A 和 B 的 右子节点 是否相等，即 recur(A.right, B.right) ；

isSubStructure(A, B) 函数：

特例处理： 当树 A 为空或树 B 为空时，直接返回 $false$ ；
返回值： 若树 B 是树 A 的子结构，则必满足以下三种情况之一，因此用或 || 连接；
1. 以 节点 A 为根节点的子树 包含树 B ，对应 recur(A, B)；
2. 树 B 是 树 A 左子树 的子结构，对应 isSubStructure(A.left, B)；
3. 树 B 是 树 A 右子树 的子结构，对应 isSubStructure(A.right, B)；
以上 2. 3. 实质上是在对树 A 做 先序遍历 。

<,,,,,,,>

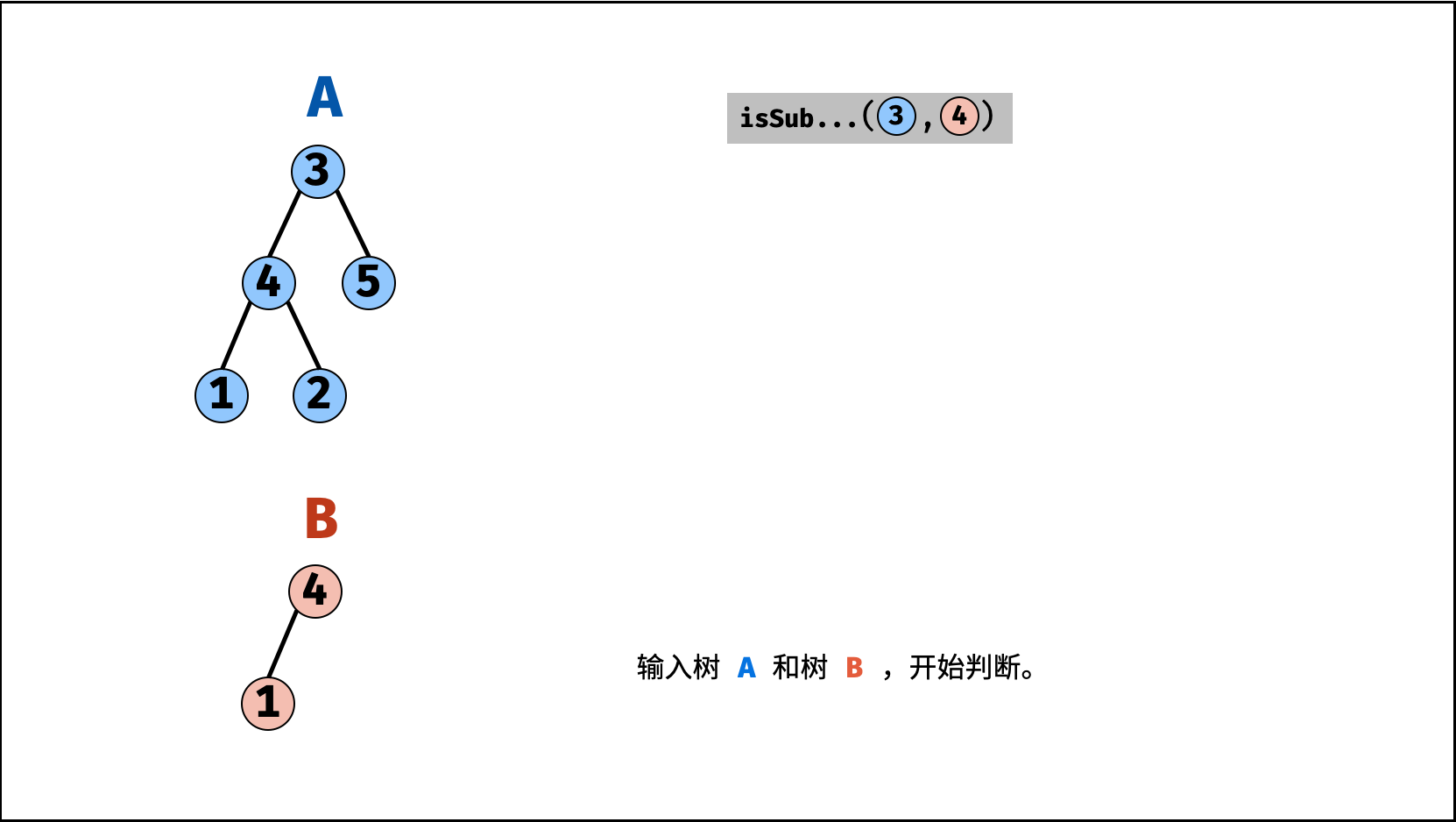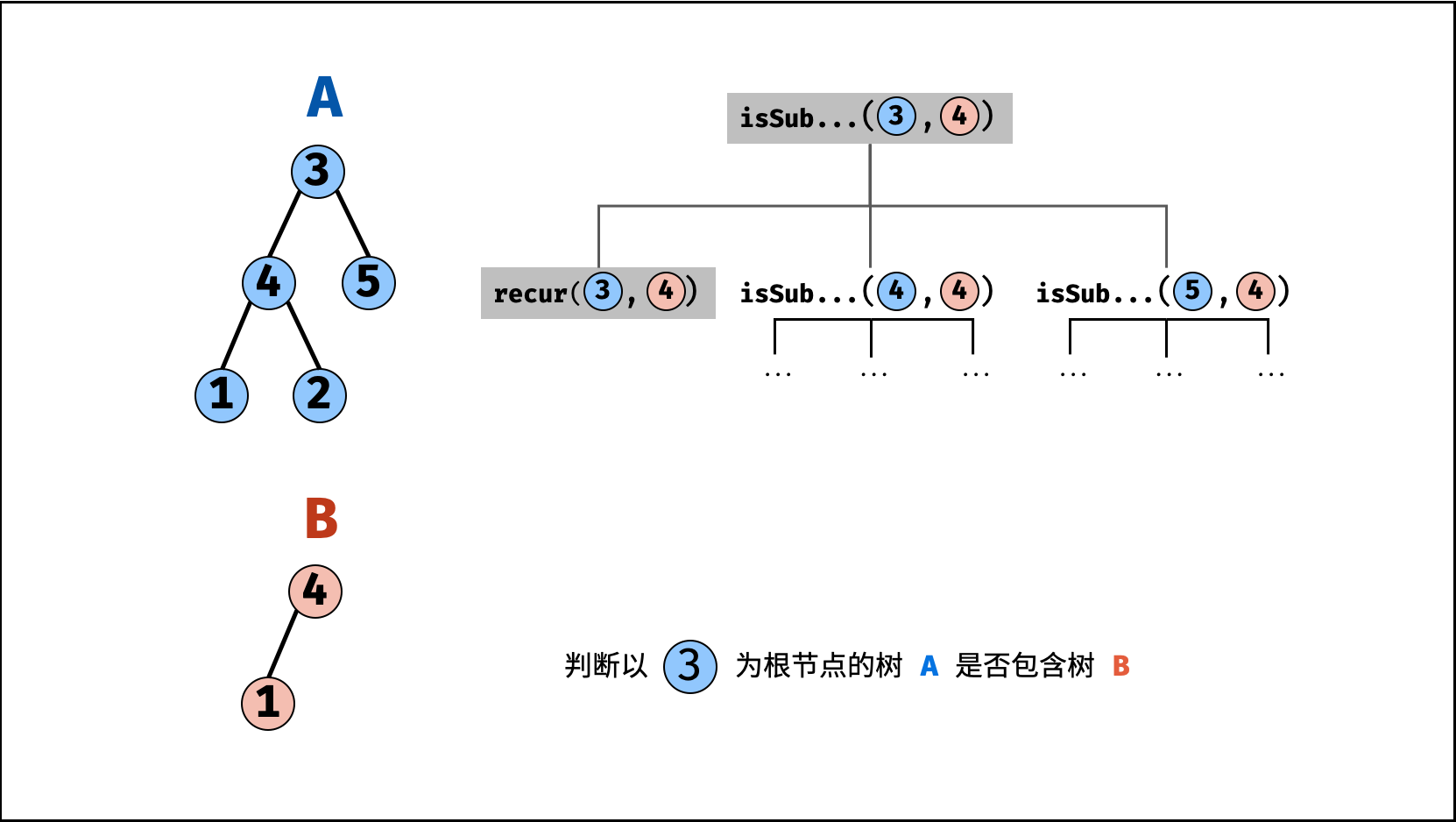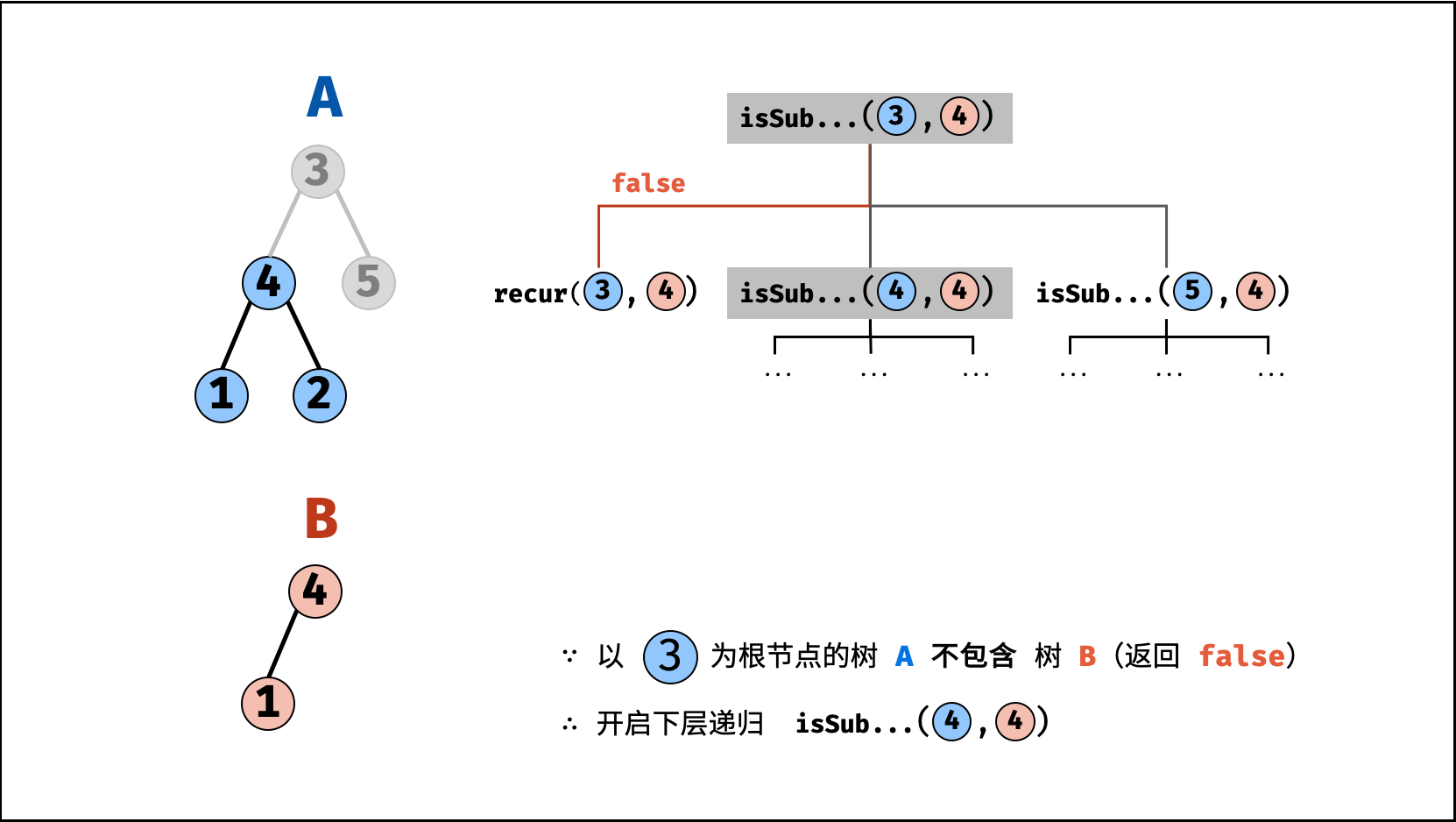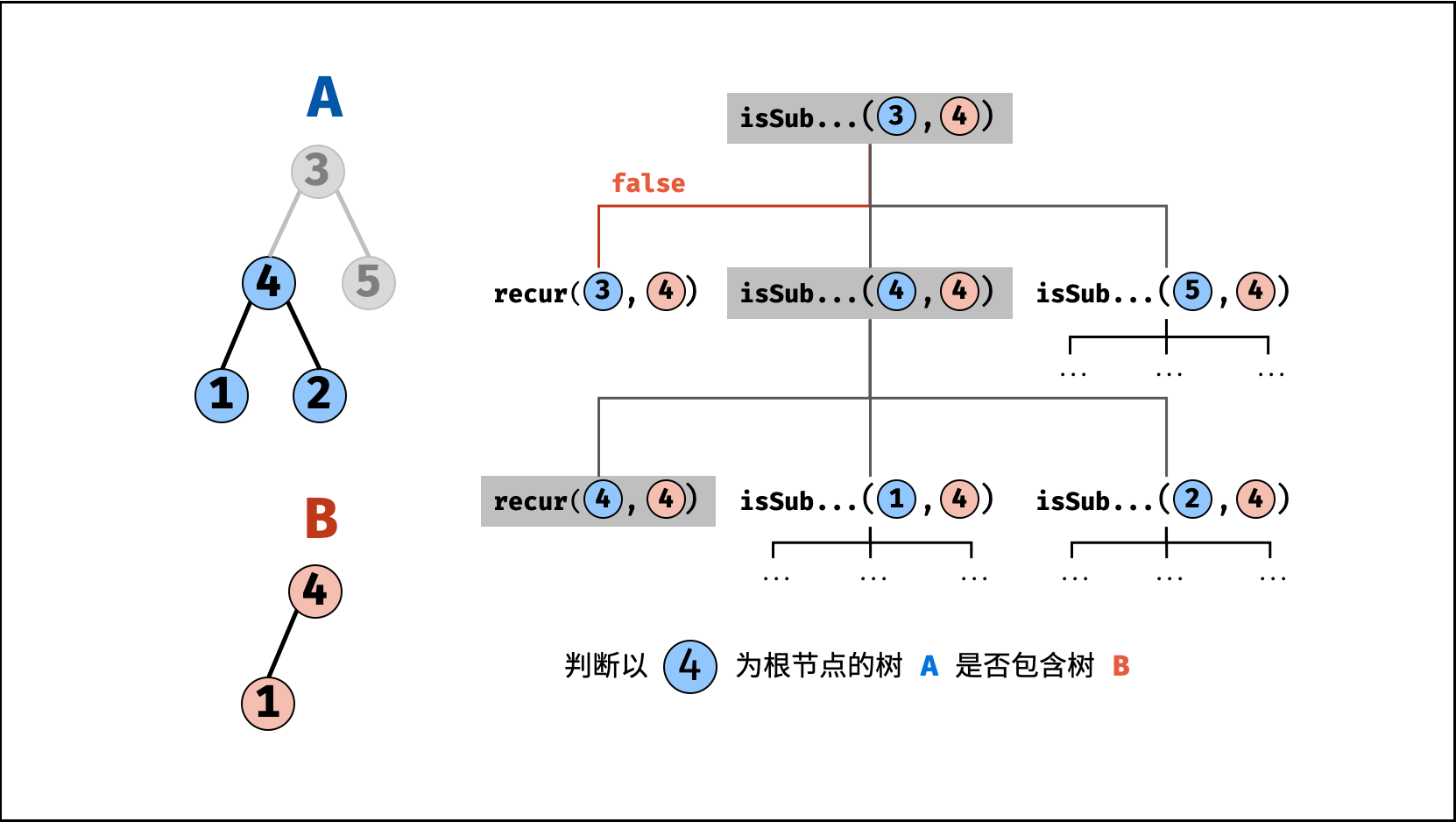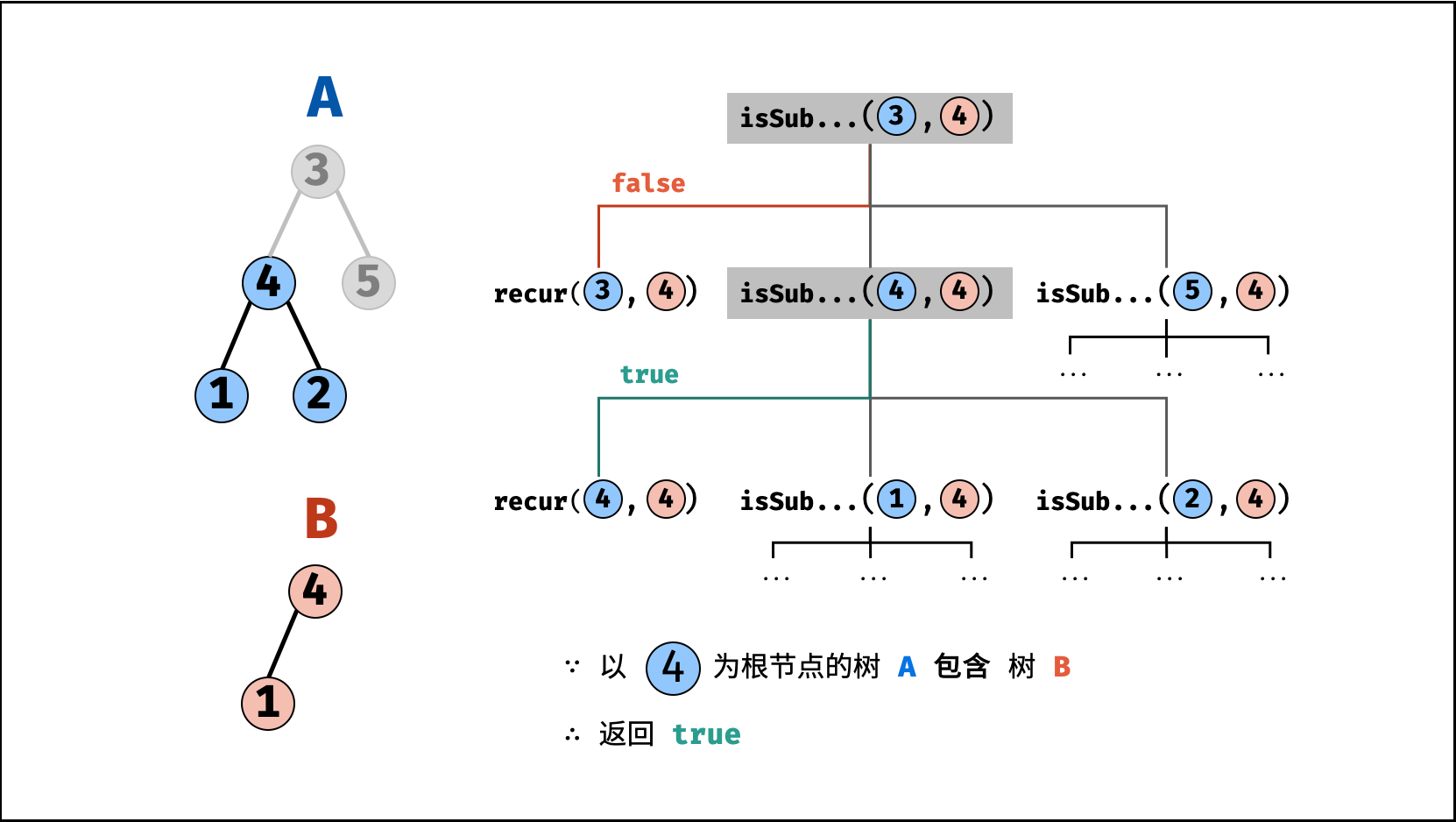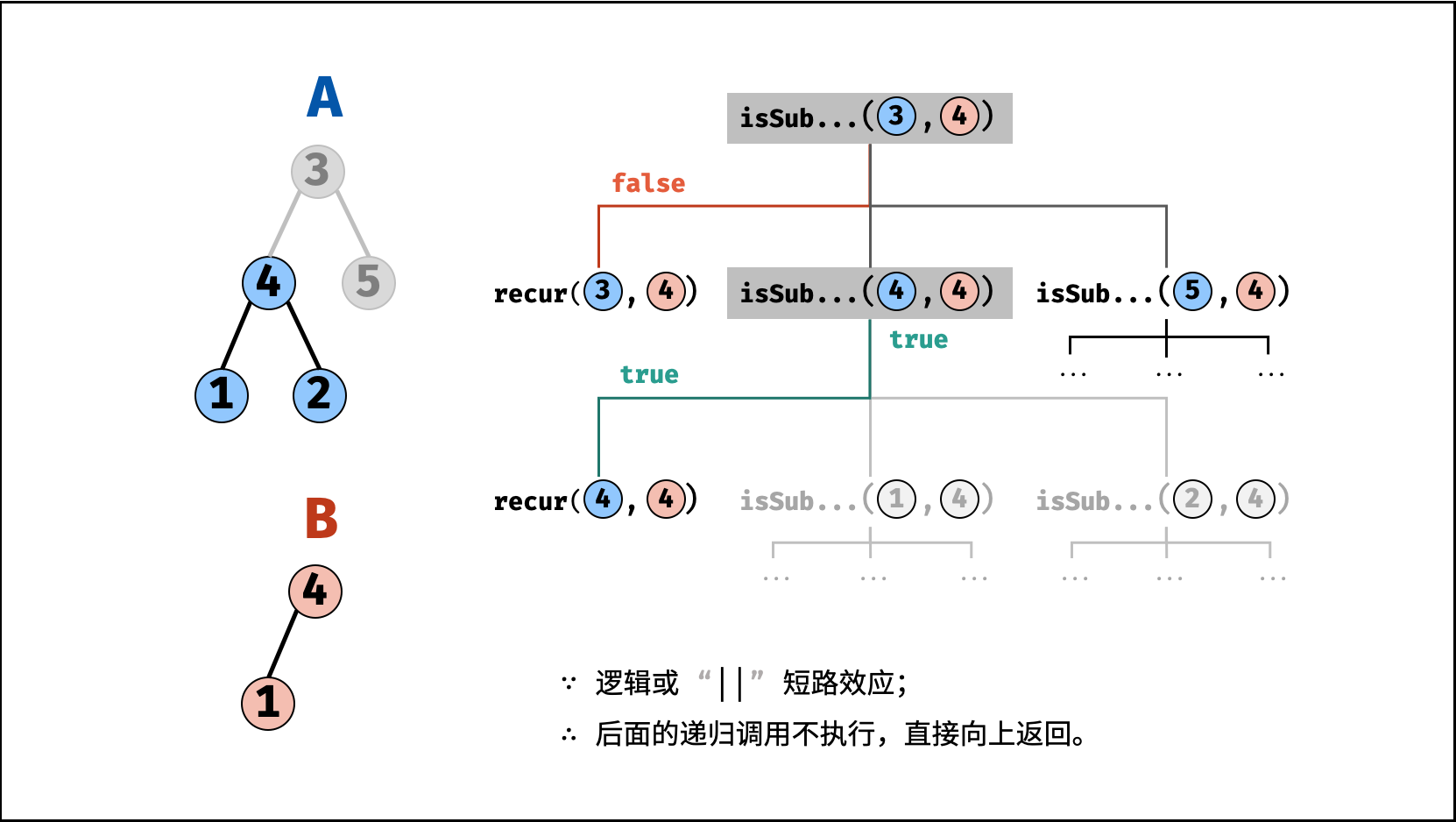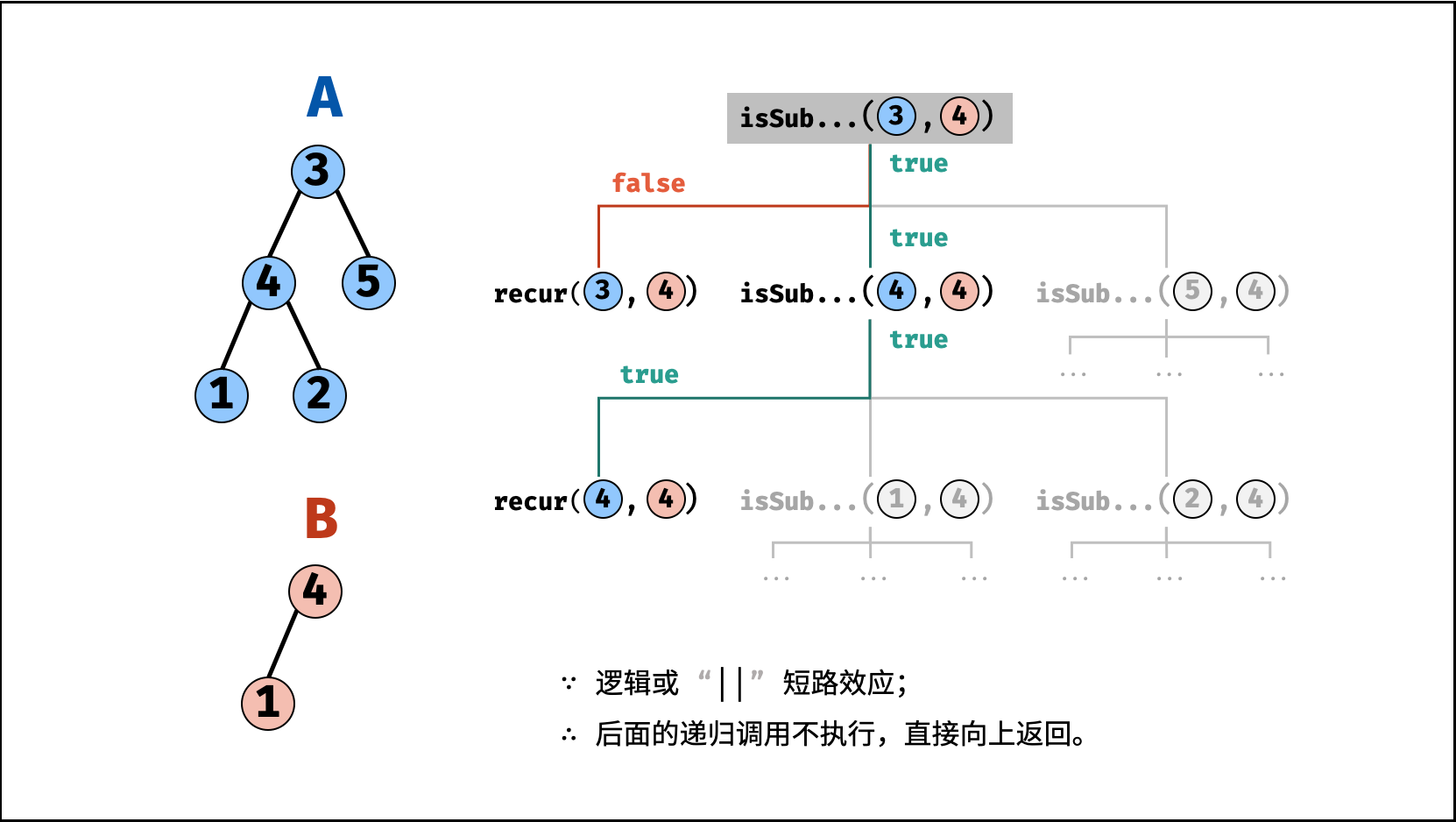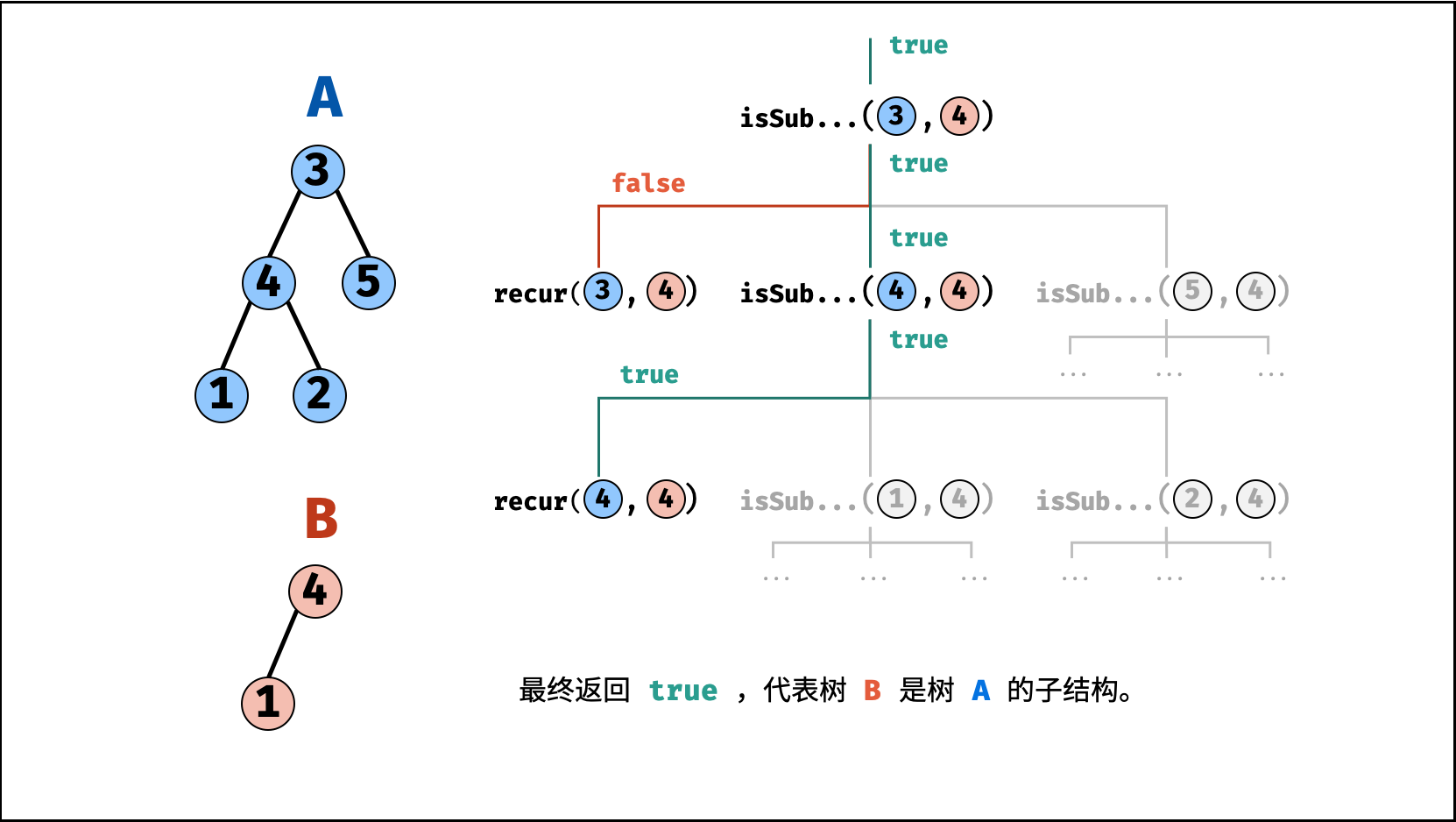复杂度分析：

时间复杂度 $O(MN)$ ： 其中 $M, N$ 分别为树 A 和树 B 的节点数量；先序遍历树 A 占用 $O(M)$ ，每次调用 recur(A, B) 判断占用 $O(N)$ 。
空间复杂度 $O(M)$ ： 当树 A 和树 B 都退化为链表时，递归调用深度最大。当 $M \leq N$ 时，遍历树 A 与递归判断的总递归深度为 $M$ ；当 $M>N$ 时，最差情况为遍历至树 A 的叶节点，此时总递归深度为 $M$。

代码：

Python

class Solution:
    def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool:
        def recur(A, B):
            if not B: return True
            if not A or A.val != B.val: return False
            return recur(A.left, B.left) and recur(A.right, B.right)

        return bool(A and B) and (recur(A, B) or self.isSubStructure(A.left, B) or self.isSubStructure(A.right, B))

Java

class Solution {
    public boolean isSubStructure(TreeNode A, TreeNode B) {
        return (A != null && B != null) && (recur(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B));
    }
    boolean recur(TreeNode A, TreeNode B) {
        if(B == null) return true;
        if(A == null || A.val != B.val) return false;
        return recur(A.left, B.left) && recur(A.right, B.right);
    }
}

C++

class Solution {
public:
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        return (A != nullptr && B != nullptr) && (recur(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B));
    }
private:
    bool recur(TreeNode* A, TreeNode* B) {
        if(B == nullptr) return true;
        if(A == nullptr || A->val != B->val) return false;
        return recur(A->left, B->left) && recur(A->right, B->right);
    }
};

解题思路： ​

算法流程： ​

复杂度分析： ​

代码： ​

解题思路：

算法流程：

复杂度分析：

代码：