解题思路： ​

设共有 $n$ 天，第 $a$ 天买，第 $b$ 天卖，则需保证 $a < b$ ；可推出交易方案数共有：

$$ (n - 1) + (n - 2) + \cdots + 2 + 1 = n(n - 1) / 2 $$

因此，暴力法的时间复杂度为 $O(n^2)$ 。考虑使用动态规划降低时间复杂度。

动态规划解析： ​

• 状态定义： 设动态规划列表 $dp$ ，$dp[i]$ 代表以 $prices[i]$ 为结尾的子数组的最大利润（以下简称为 前 $i$ 日的最大利润 ）。
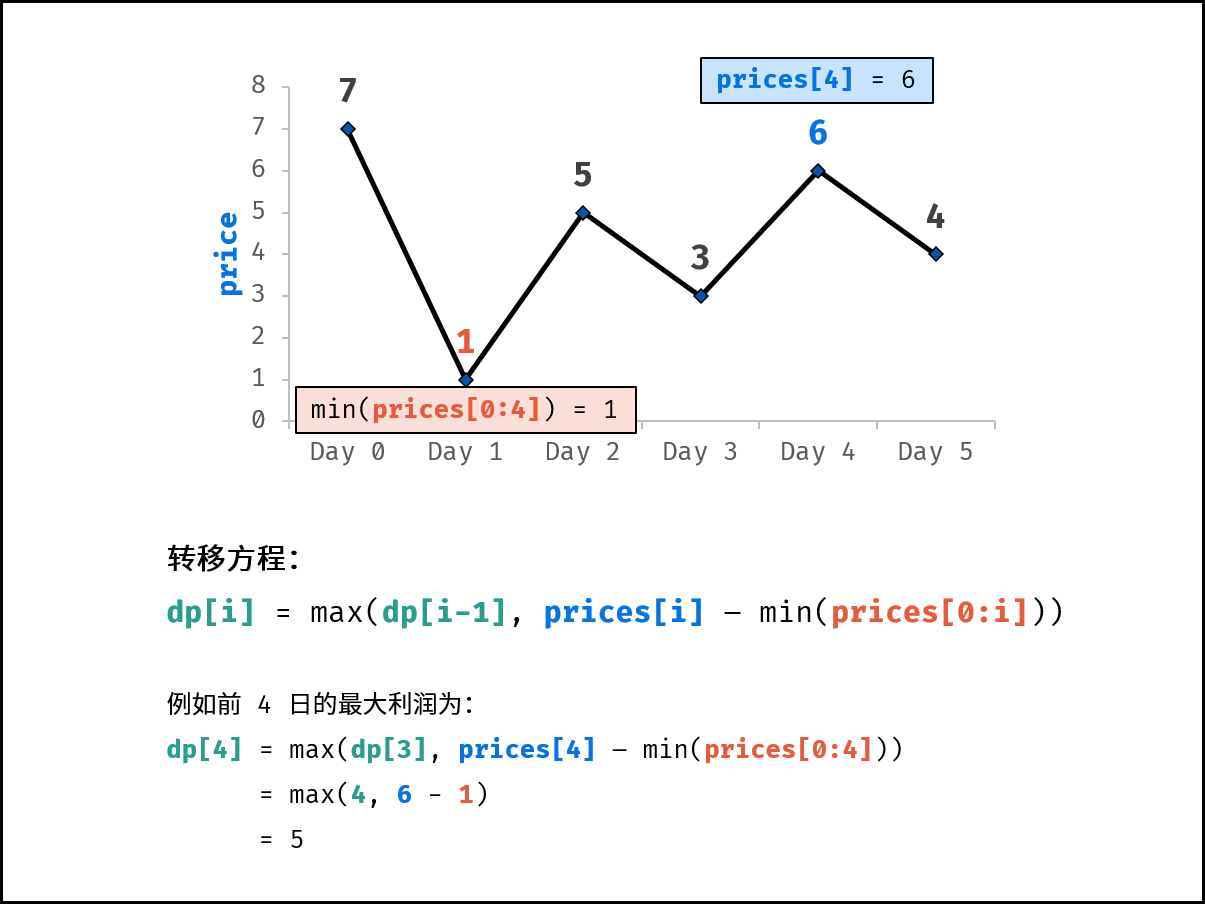
• 转移方程： 由于题目限定 “买卖该股票一次” ，因此前 $i$ 日最大利润 $dp[i]$ 等于前 $i - 1$ 日最大利润 $dp[i-1]$ 和第 $i$ 日卖出的最大利润中的最大值。

$$ dp[i] = \max(dp[i - 1], prices[i] - \min(prices[0:i])) \

↑ \

前 i 日最大利润 = \max(前 (i-1) 日最大利润, 第 i 日价格 - 前 i 日最低价格) $$

• 初始状态： $dp[0] = 0$ ，即首日利润为 $0$ ；
• 返回值： $dp[n - 1]$ ，其中 $n$ 为 $dp$ 列表长度。

时间复杂度降低： ​

前 $i$ 日的最低价格 $\min(prices[0:i])$ 时间复杂度为 $O(i)$ 。而在遍历 $prices$ 时，可以借助一个变量（记为成本 $cost$ ）每日更新最低价格。优化后的转移方程为：

$$ dp[i] = \max(dp[i - 1], prices[i] - \min(cost, prices[i]) $$

空间复杂度降低： ​

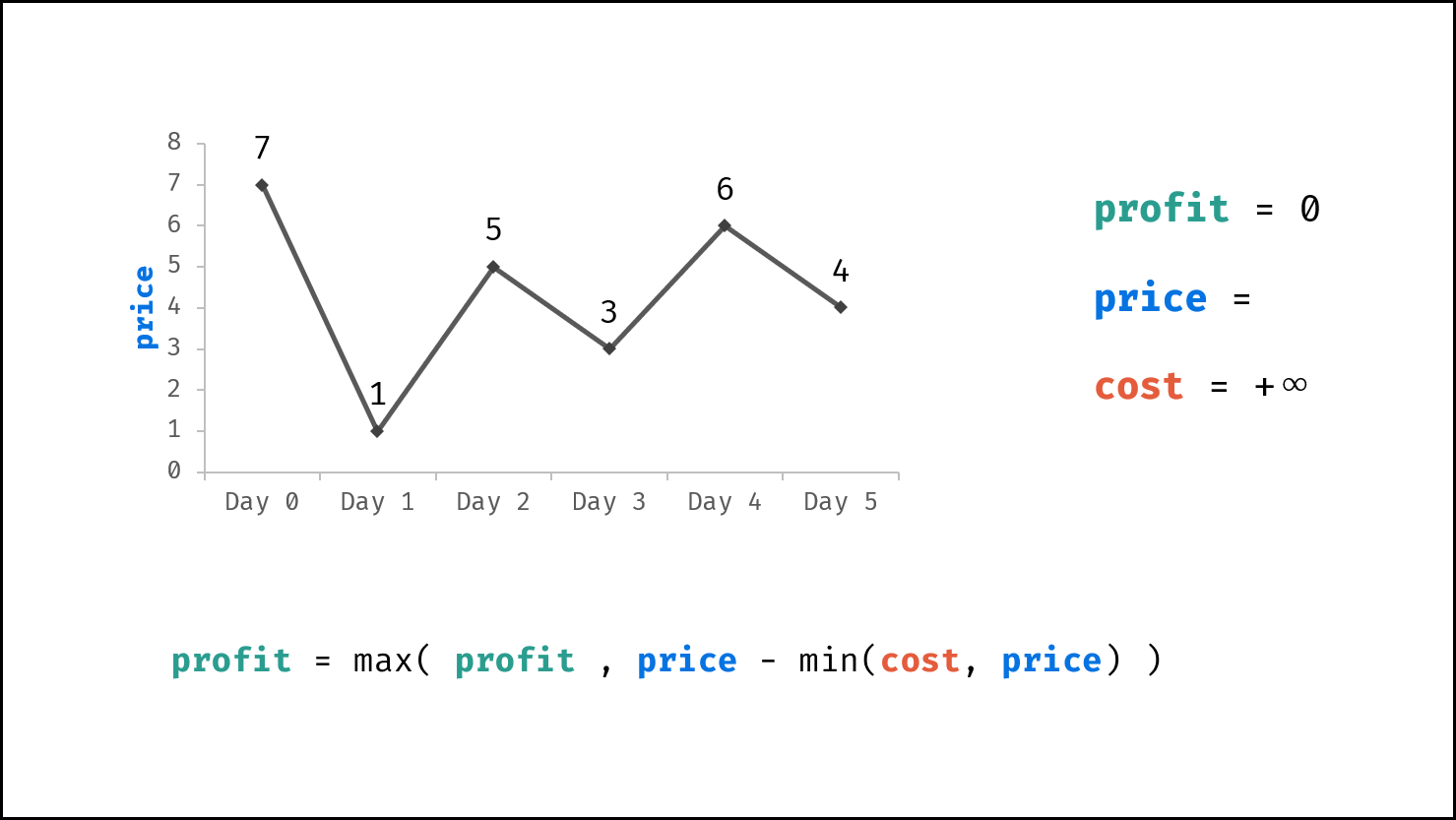
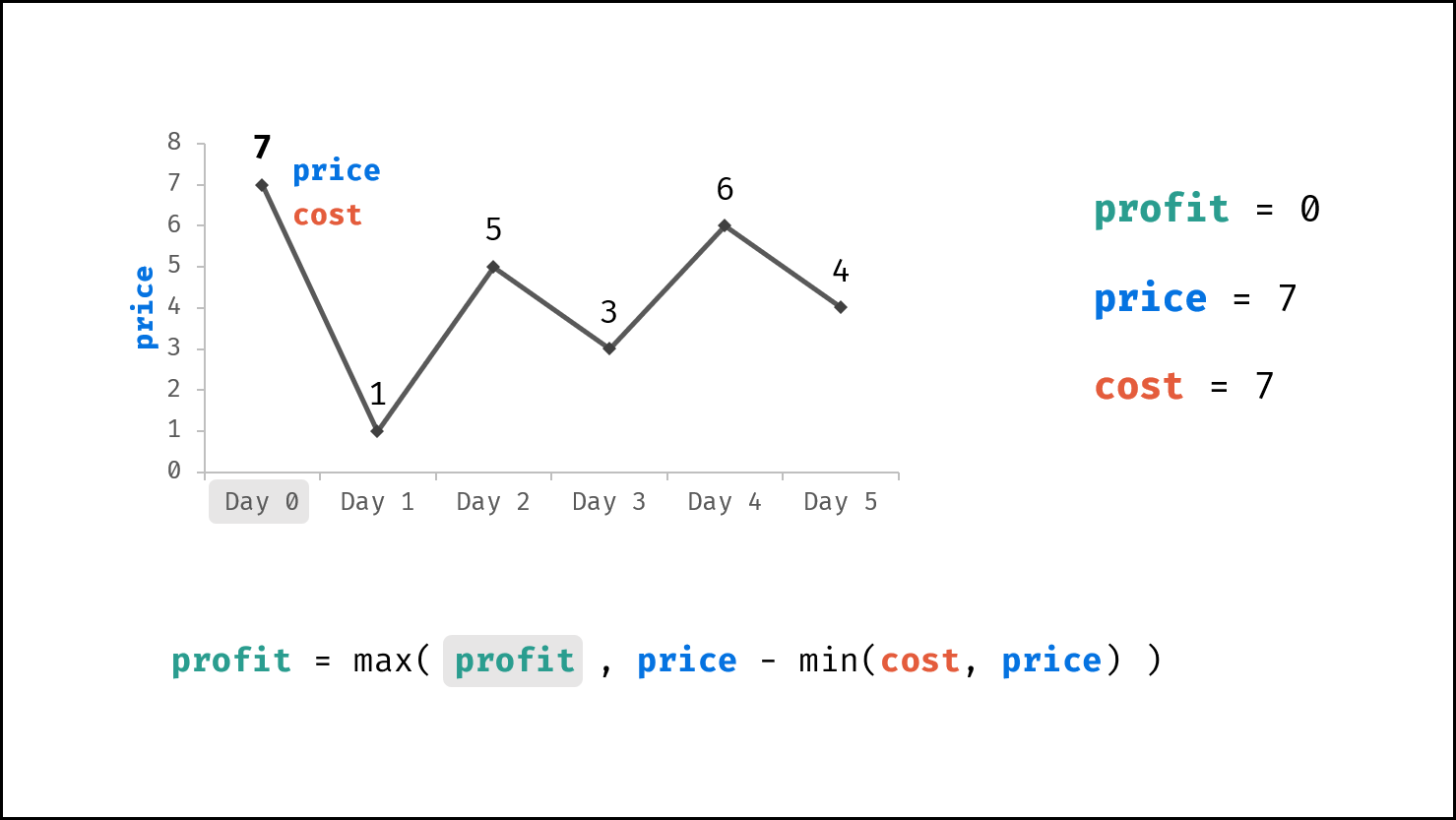
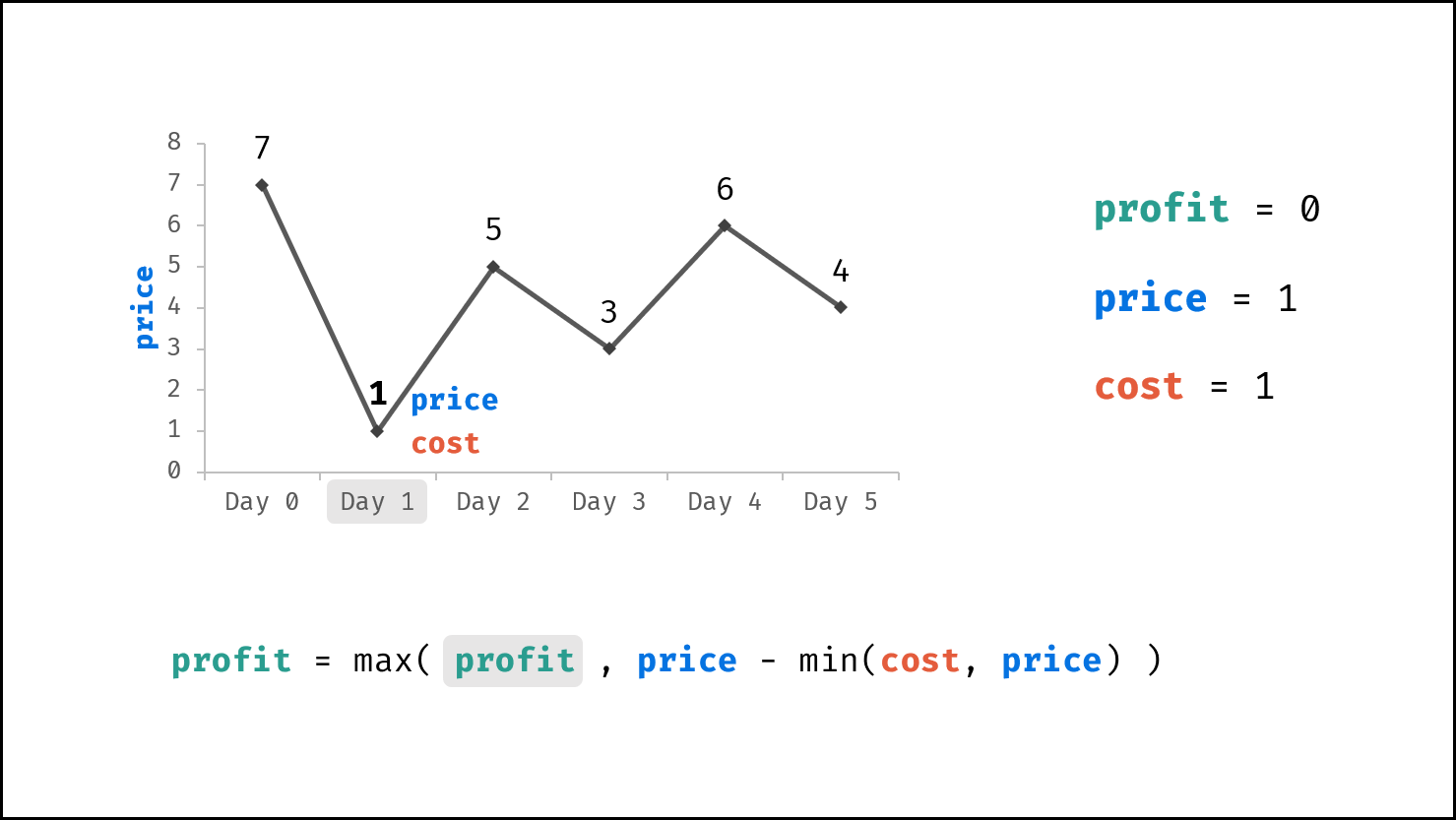
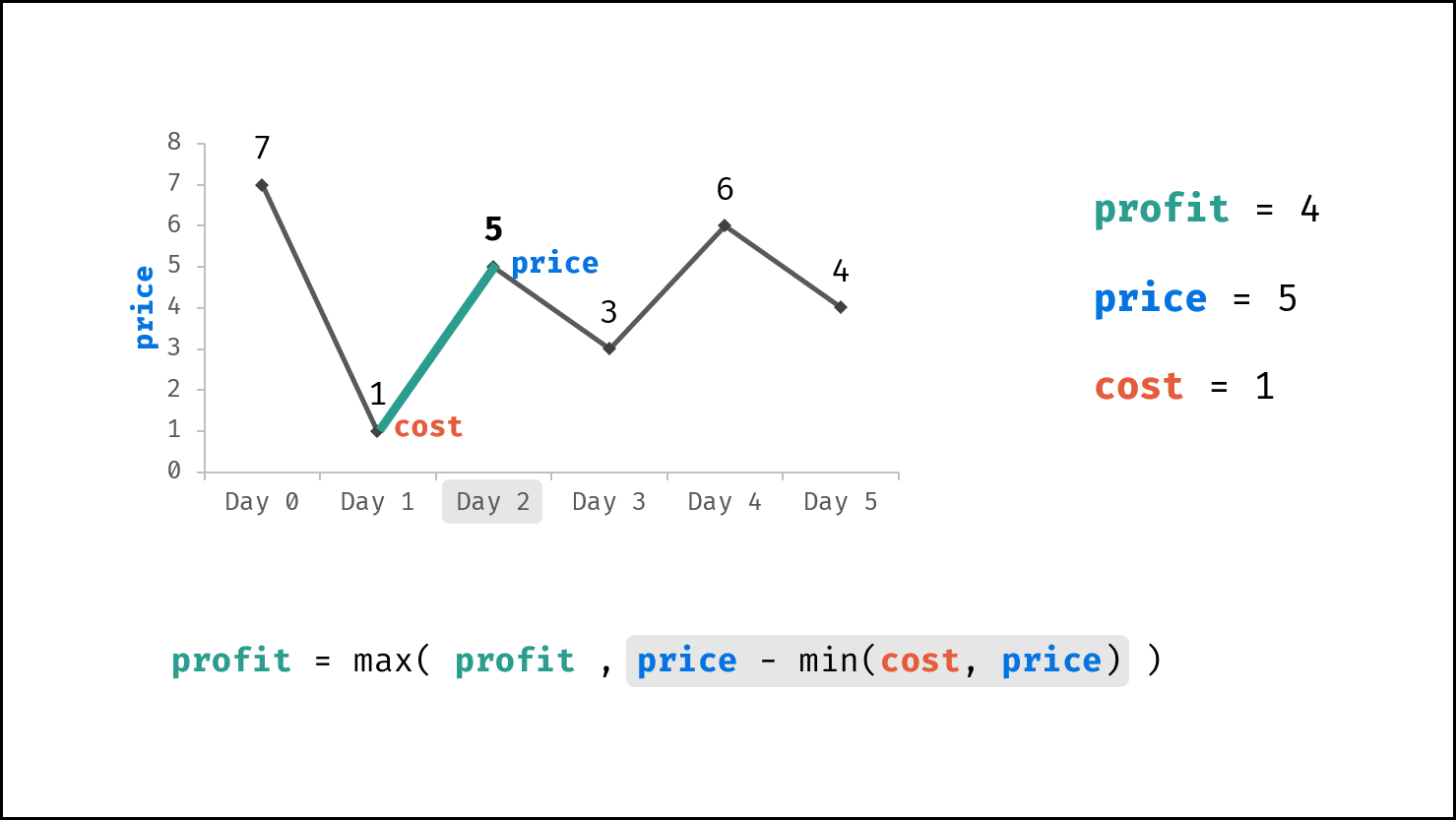
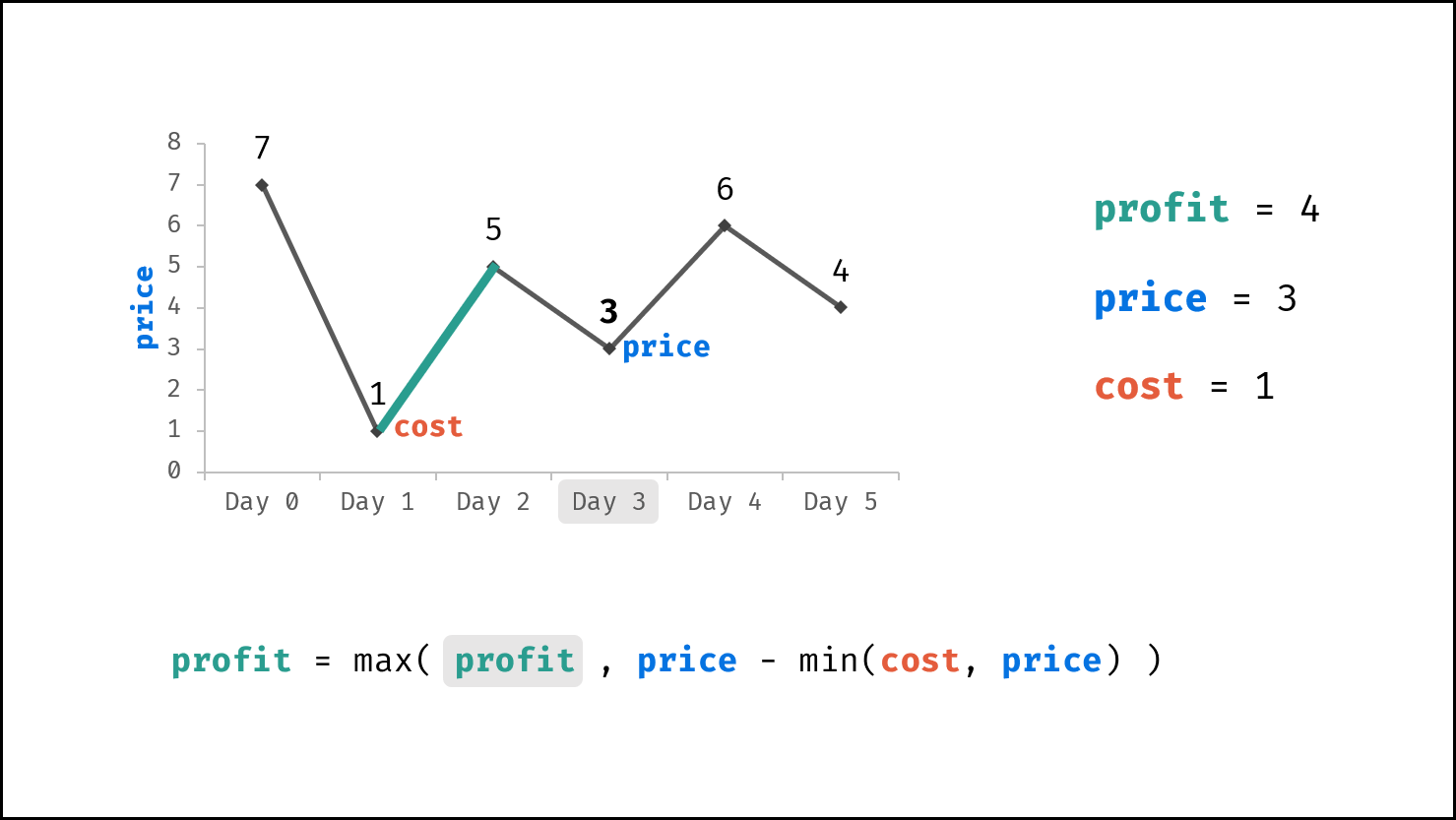
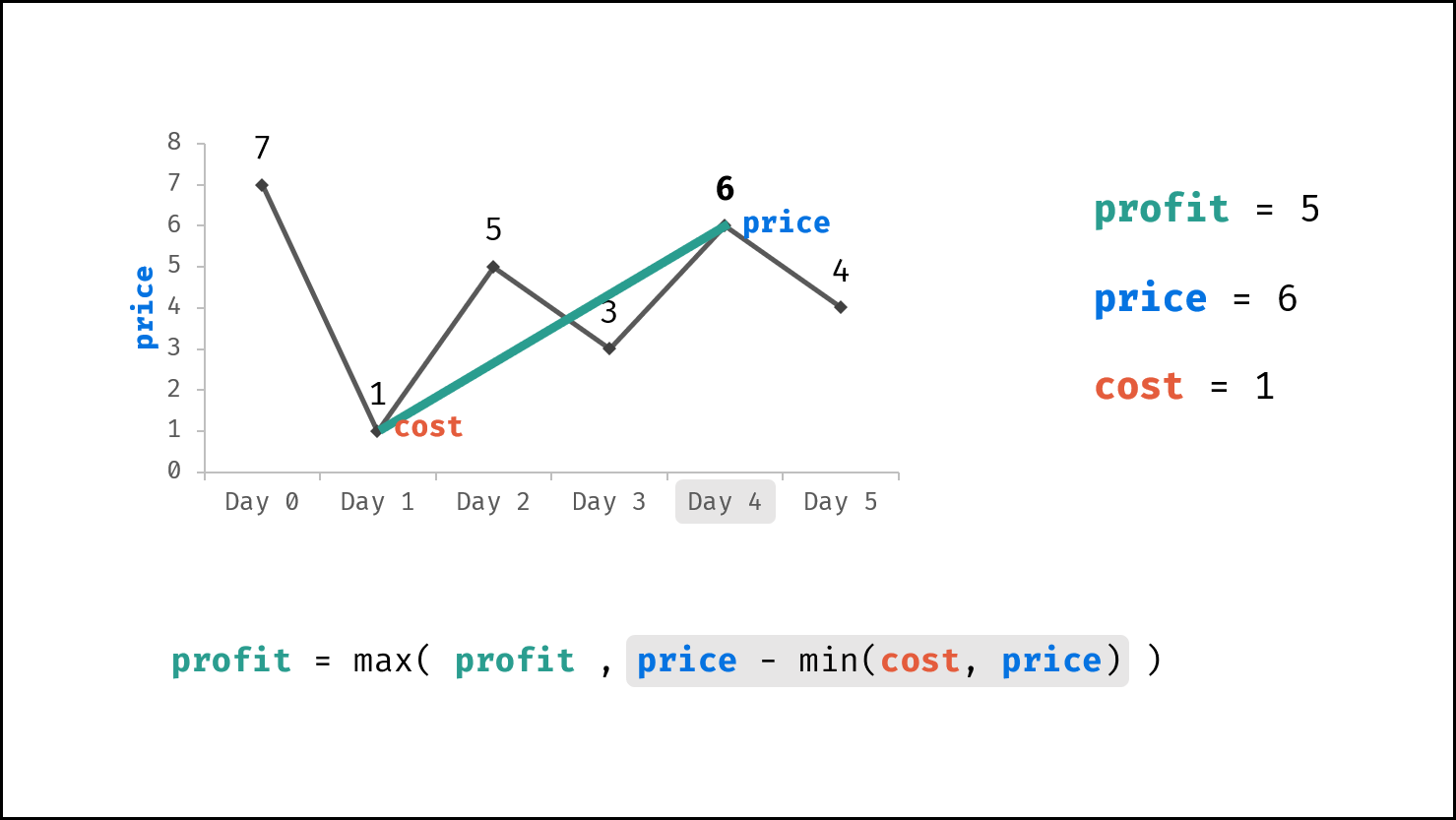
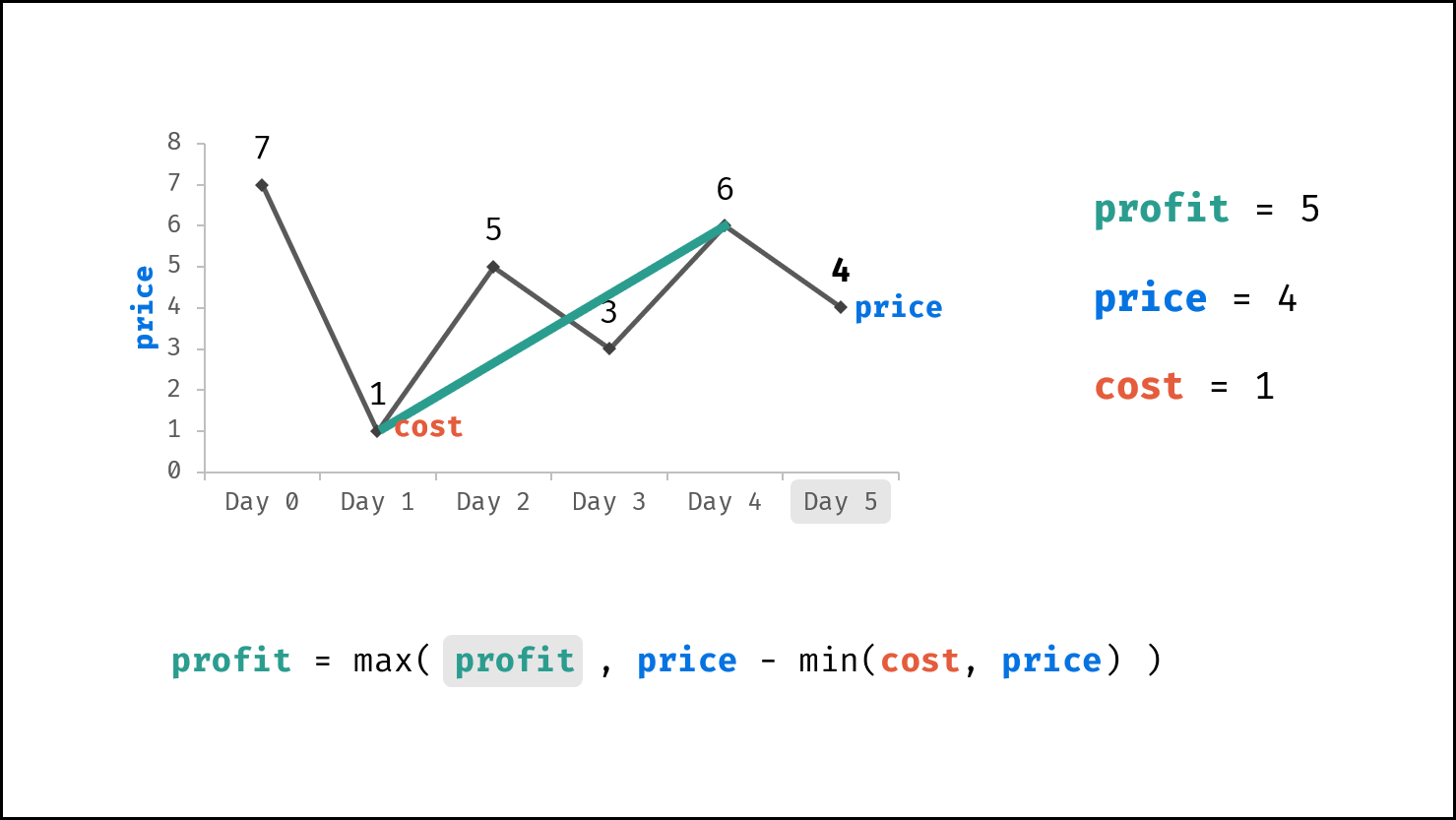
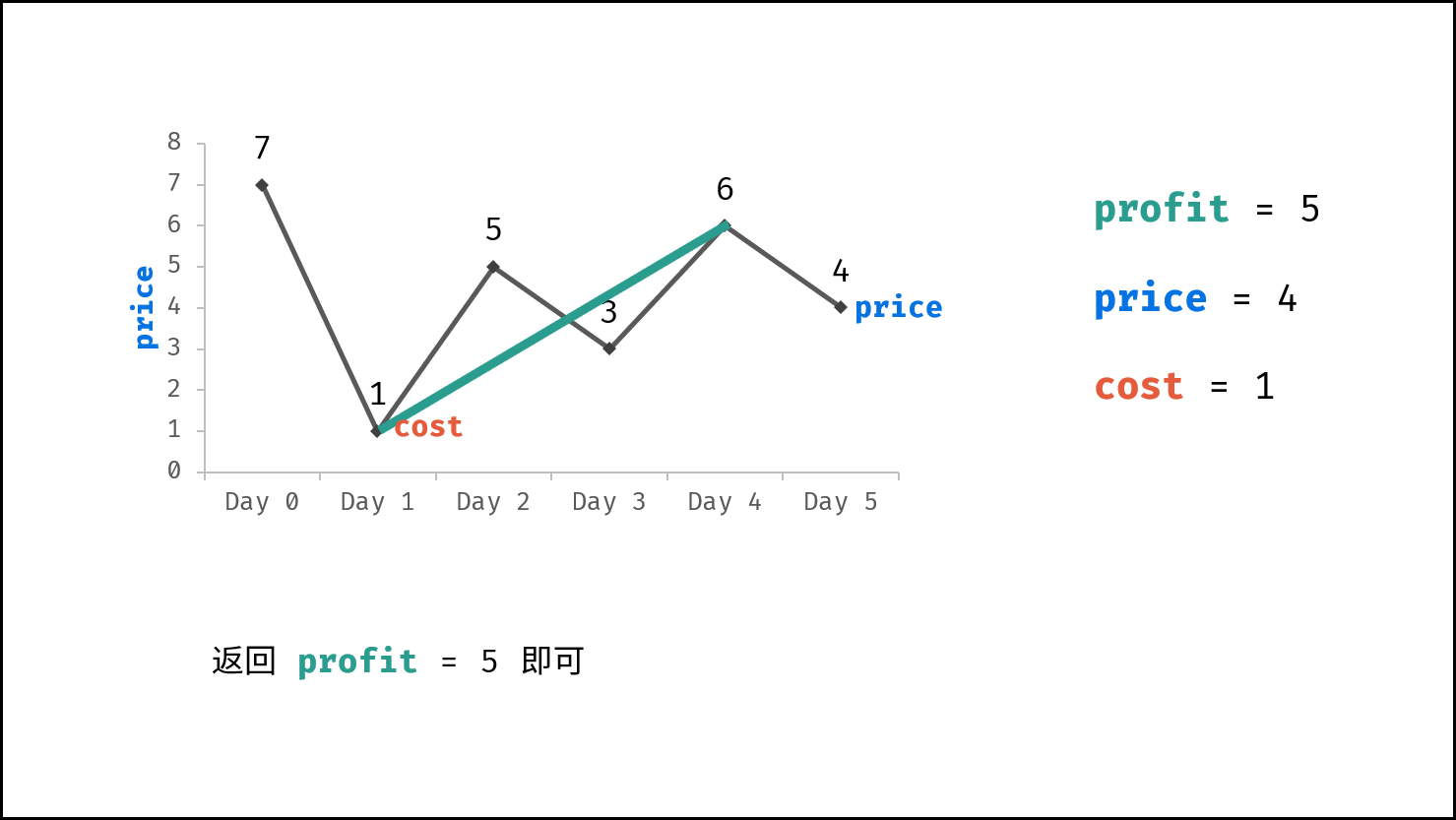
由于 $dp[i]$ 只与 $dp[i - 1]$ , $prices[i]$ , $cost$ 相关，因此可使用一个变量（记为利润 $profit$ ）代替 $dp$ 列表。优化后的转移方程为：

$$ profit = \max(profit, prices[i] - \min(cost, prices[i]) $$

复杂度分析： ​

• 时间复杂度 $O(N)$ ： 其中 $N$ 为 $prices$ 列表长度，动态规划需遍历 $prices$ 。
• 空间复杂度 $O(1)$ ： 变量 $cost$ 和 $profit$ 使用常数大小的额外空间。

<,,,,,,,>

代码： ​

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        cost, profit = float("+inf"), 0
        for price in prices:
            cost = min(cost, price)
            profit = max(profit, price - cost)
        return profit

class Solution {
    public int maxProfit(int[] prices) {
        int cost = Integer.MAX_VALUE, profit = 0;
        for(int price : prices) {
            cost = Math.min(cost, price);
            profit = Math.max(profit, price - cost);
        }
        return profit;
    }
}

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int cost = INT_MAX, profit = 0;
        for(int price : prices) {
            cost = min(cost, price);
            profit = max(profit, price - cost);
        }
        return profit;
    }
};