解题思路:
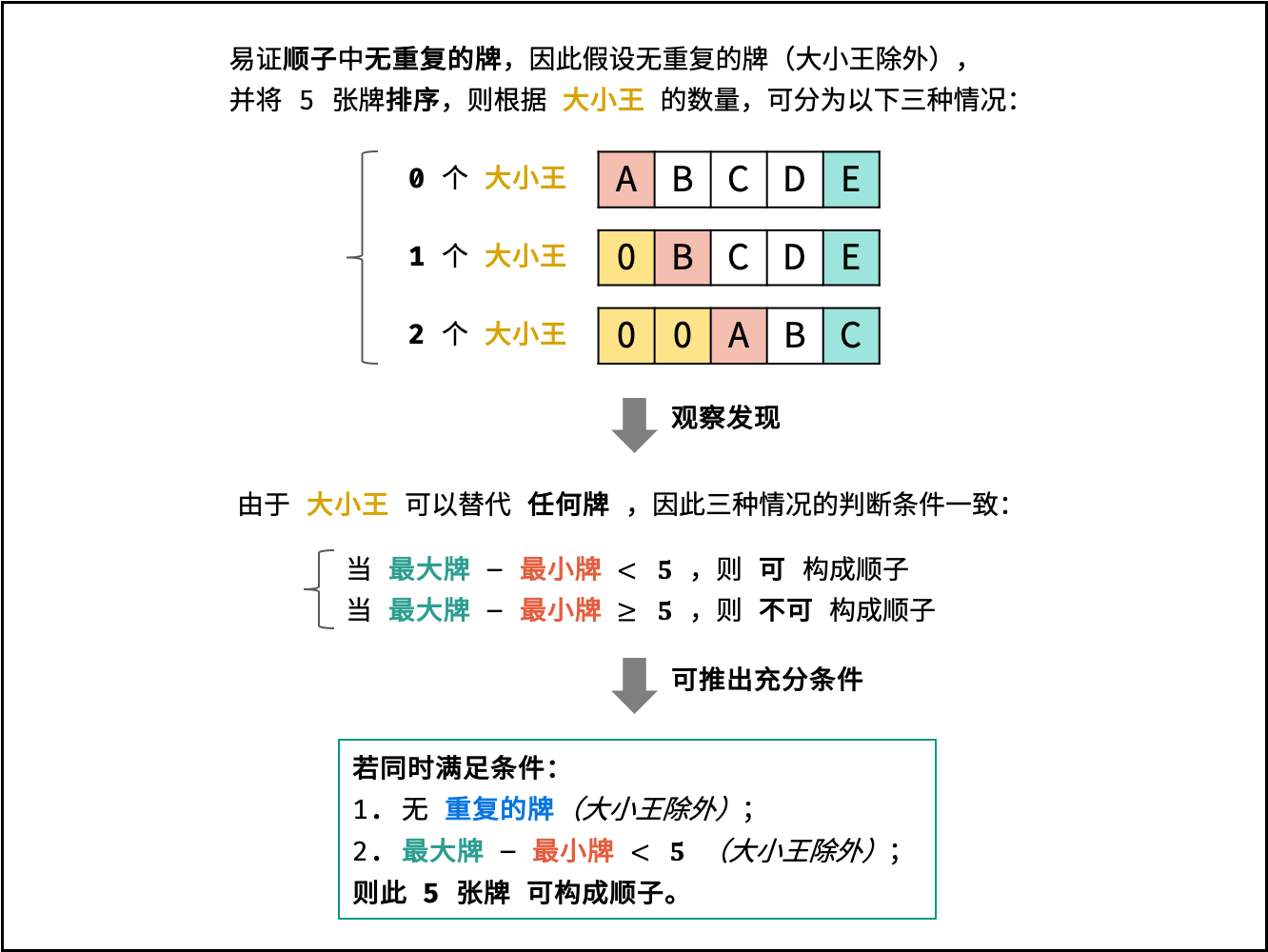
根据题意,此 $5$ 张牌是顺子的 充分条件 如下:
- 除大小王外,所有牌 无重复 ;
- 设此 $5$ 张牌中最大的牌为 $max$ ,最小的牌为 $min$ (大小王除外),则需满足:
$$ max - min < 5 $$
因此可将问题转化为:此 $5$ 张牌是否满足以上两个条件?
方法一: 集合 Set + 遍历
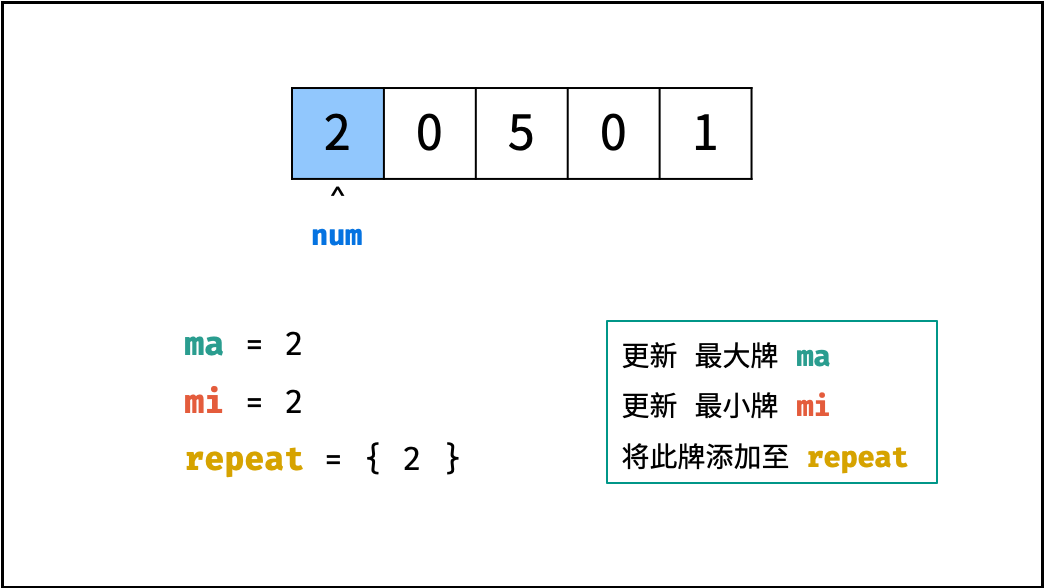
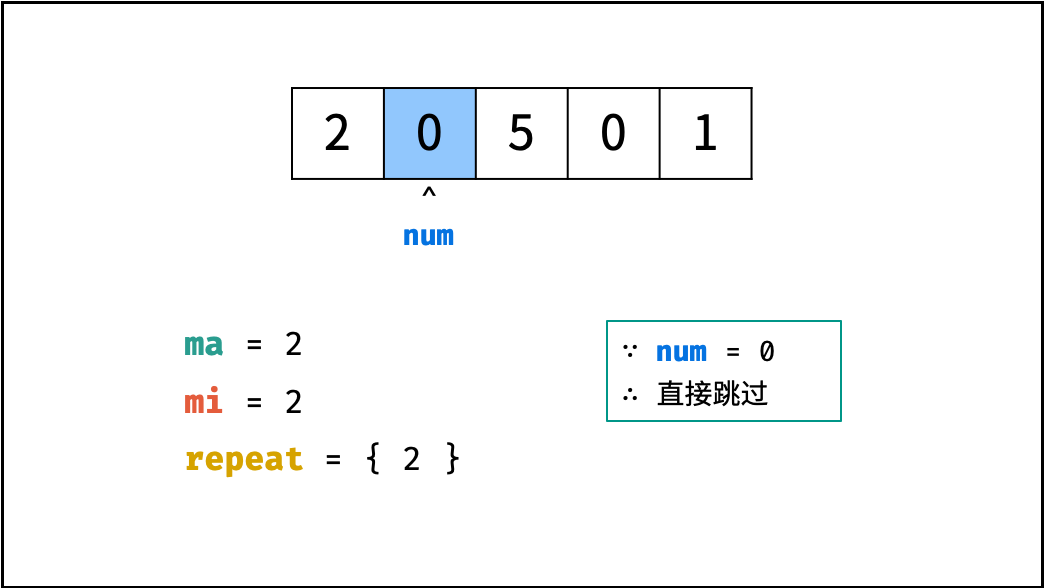
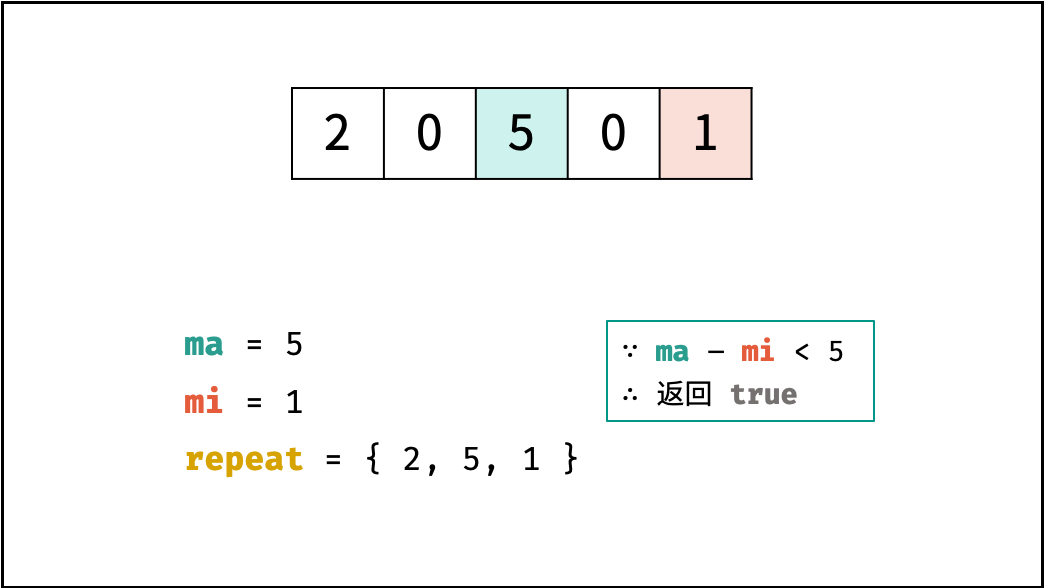
- 遍历五张牌,遇到大小王(即 $0$ )直接跳过。
- 判别重复: 利用 Set 实现遍历判重, Set 的查找方法的时间复杂度为 $O(1)$ ;
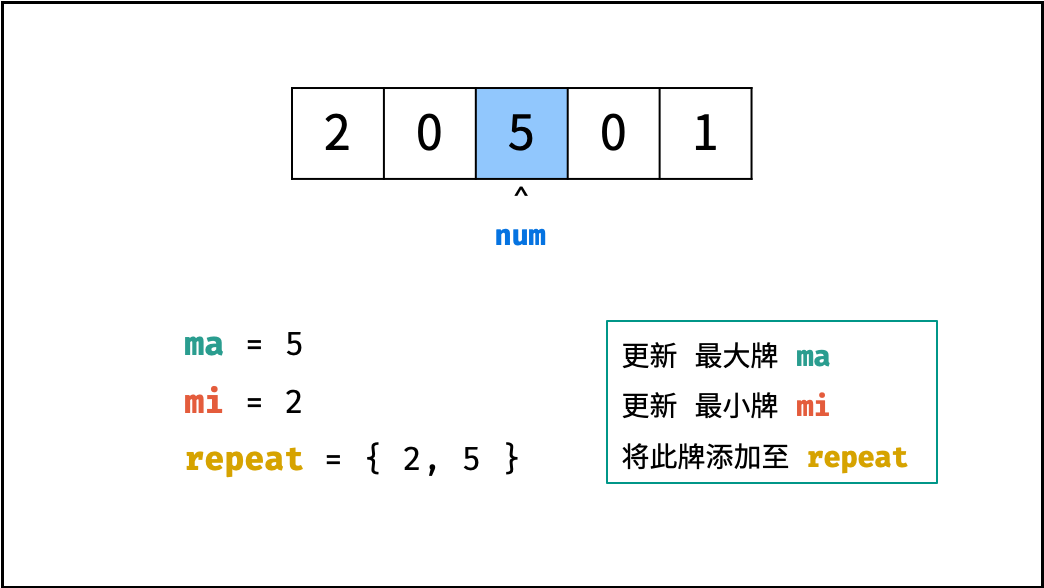
- 获取最大 / 最小的牌: 借助辅助变量 $ma$ 和 $mi$ ,遍历统计即可。
复杂度分析:
- 时间复杂度 $O(1)$ : 本题中给定牌数量 $N \equiv 5$ ;遍历数组使用 $O(N) = O(5) = O(1)$ 时间。
- 空间复杂度 $O(1)$ : 用于判重的辅助 Set 使用 $O(N) = O(1)$ 额外空间。
< ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码:
Python
class Solution:
def isStraight(self, nums: List[int]) -> bool:
repeat = set()
ma, mi = 0, 14
for num in nums:
if num == 0: continue # 跳过大小王
ma = max(ma, num) # 最大牌
mi = min(mi, num) # 最小牌
if num in repeat: return False # 若有重复,提前返回 false
repeat.add(num) # 添加牌至 Set
return ma - mi < 5 # 最大牌 - 最小牌 < 5 则可构成顺子Java
class Solution {
public boolean isStraight(int[] nums) {
Set<Integer> repeat = new HashSet<>();
int max = 0, min = 14;
for(int num : nums) {
if(num == 0) continue; // 跳过大小王
max = Math.max(max, num); // 最大牌
min = Math.min(min, num); // 最小牌
if(repeat.contains(num)) return false; // 若有重复,提前返回 false
repeat.add(num); // 添加此牌至 Set
}
return max - min < 5; // 最大牌 - 最小牌 < 5 则可构成顺子
}
}C++
class Solution {
public:
bool isStraight(vector<int>& nums) {
unordered_set<int> repeat;
int ma = 0, mi = 14;
for(int num : nums) {
if(num == 0) continue; // 跳过大小王
ma = max(ma, num); // 最大牌
mi = min(mi, num); // 最小牌
if(repeat.find(num) != repeat.end()) return false; // 若有重复,提前返回 false
repeat.insert(num); // 添加此牌至 Set
}
return ma - mi < 5; // 最大牌 - 最小牌 < 5 则可构成顺子
}
};方法二:排序 + 遍历
- 先对数组执行排序。
- 判别重复: 排序数组中的相同元素位置相邻,因此可通过遍历数组,判断 $nums[i] = nums[i + 1]$ 是否成立来判重。
- 获取最大 / 最小的牌: 排序后,数组末位元素 $nums[4]$ 为最大牌;元素 $nums[joker]$ 为最小牌,其中 $joker$ 为大小王的数量。
复杂度分析:
- 时间复杂度 $O(1)$ : 本题中给定牌数量 $N \equiv 5$ ;数组排序使用 $O(N \log N) = O(5 \log 5) = O(1)$ 时间。
- 空间复杂度 $O(1)$ : 变量 $joker$ 使用 $O(1)$ 大小的额外空间。
< ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码:
Python
class Solution:
def isStraight(self, nums: List[int]) -> bool:
joker = 0
nums.sort() # 数组排序
for i in range(4):
if nums[i] == 0: joker += 1 # 统计大小王数量
elif nums[i] == nums[i + 1]: return False # 若有重复,提前返回 false
return nums[4] - nums[joker] < 5 # 最大牌 - 最小牌 < 5 则可构成顺子Java
class Solution {
public boolean isStraight(int[] nums) {
int joker = 0;
Arrays.sort(nums); // 数组排序
for(int i = 0; i < 4; i++) {
if(nums[i] == 0) joker++; // 统计大小王数量
else if(nums[i] == nums[i + 1]) return false; // 若有重复,提前返回 false
}
return nums[4] - nums[joker] < 5; // 最大牌 - 最小牌 < 5 则可构成顺子
}
}C++
class Solution {
public:
bool isStraight(vector<int>& nums) {
int joker = 0;
sort(nums.begin(), nums.end()); // 数组排序
for(int i = 0; i < 4; i++) {
if(nums[i] == 0) joker++; // 统计大小王数量
else if(nums[i] == nums[i + 1]) return false; // 若有重复,提前返回 false
}
return nums[4] - nums[joker] < 5; // 最大牌 - 最小牌 < 5 则可构成顺子
}
};