自律小屋 | 自律小屋

解题思路：

后序遍历定义： [ 左子树 | 右子树 | 根节点 ] ，即遍历顺序为 “左、右、根” 。

二叉搜索树定义： 左子树中所有节点的值 $<$ 根节点的值；右子树中所有节点的值 $>$ 根节点的值；其左、右子树也分别为二叉搜索树。

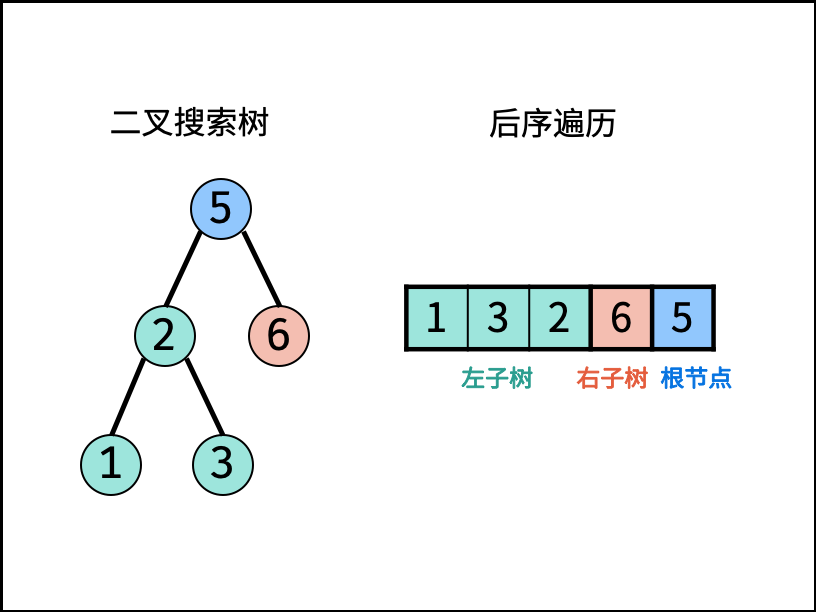
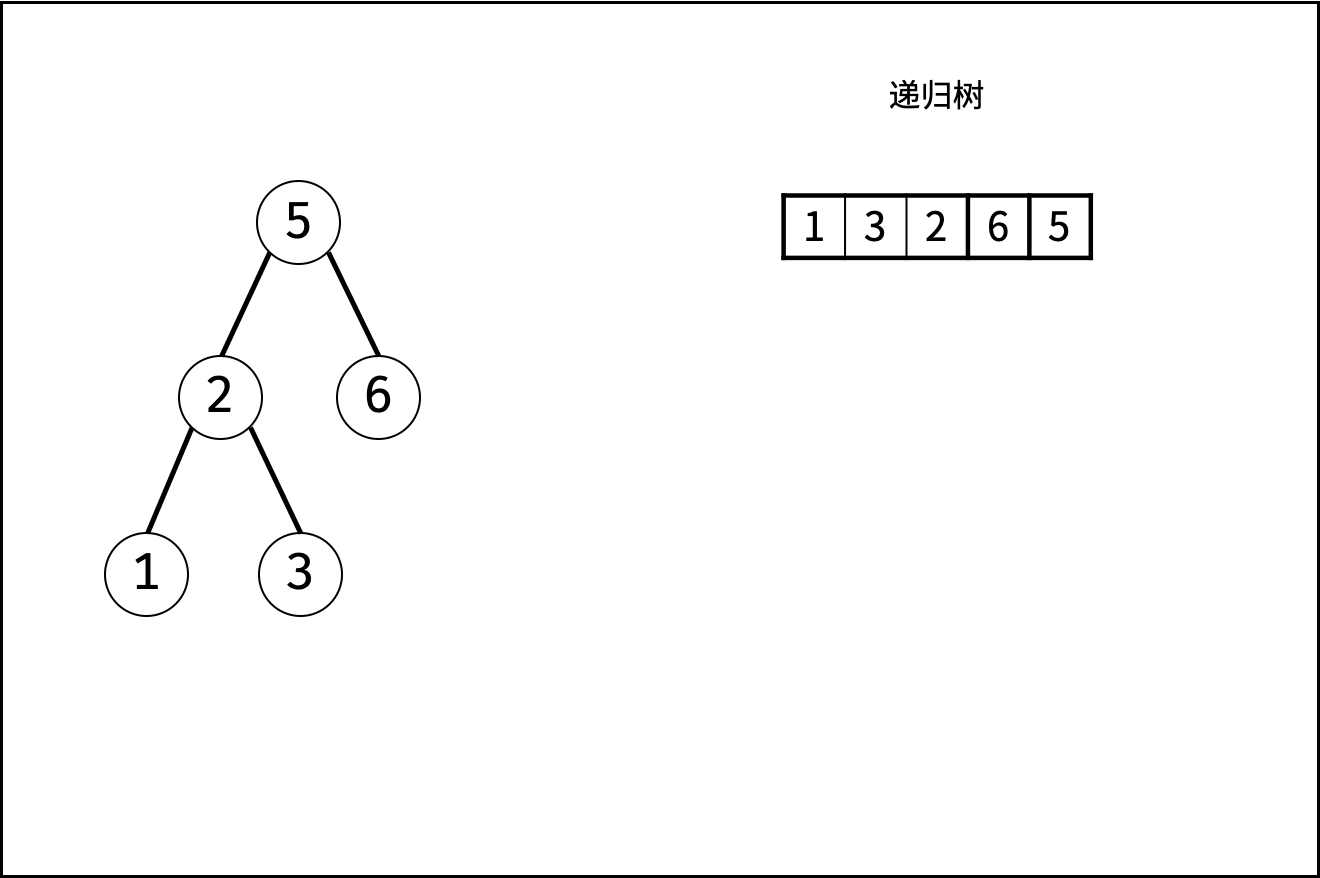
方法一：递归分治

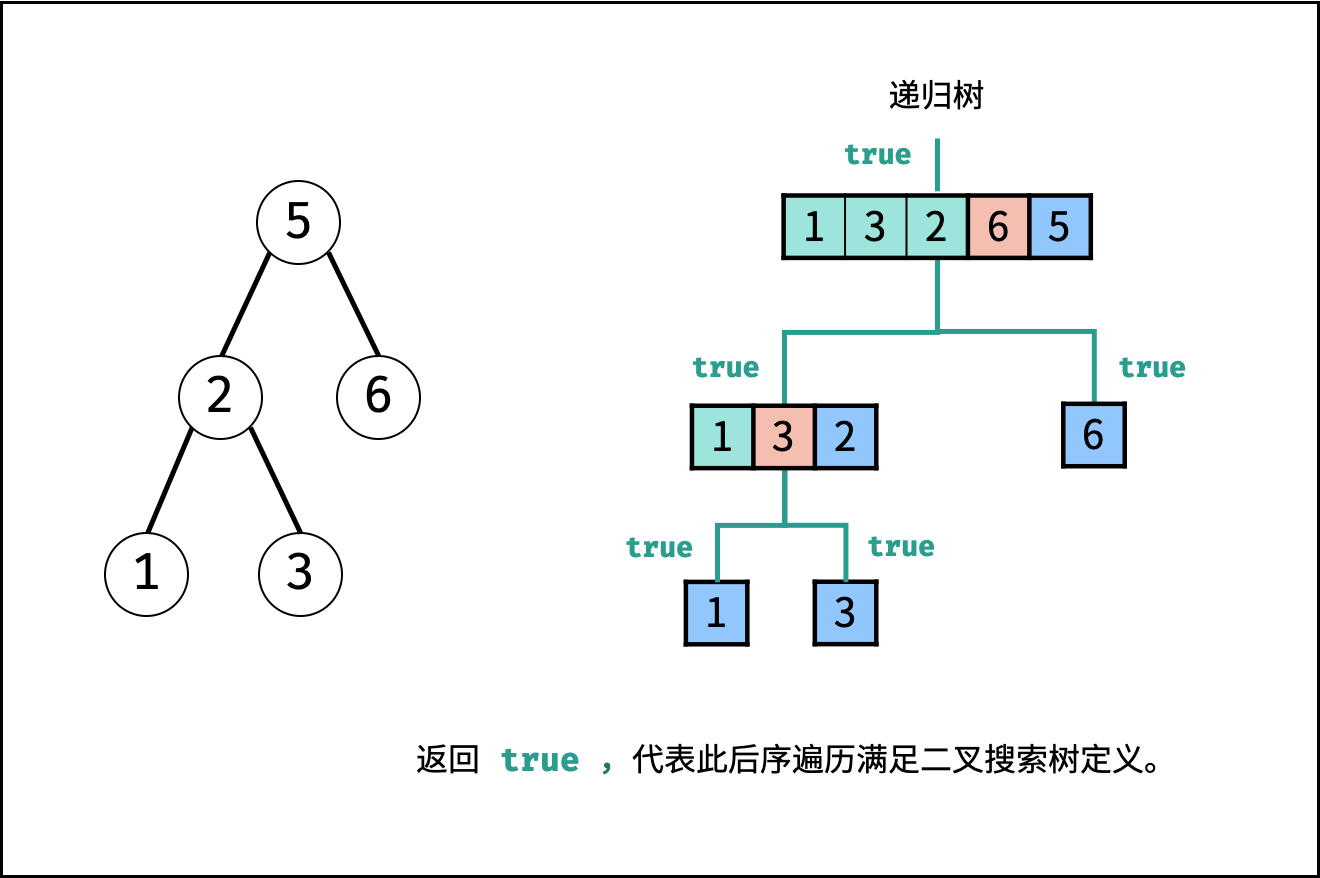
根据二叉搜索树的定义，可以通过递归，判断所有子树的 正确性 （即其后序遍历是否满足二叉搜索树的定义），若所有子树都正确，则此序列为二叉搜索树的后序遍历。

递归解析：

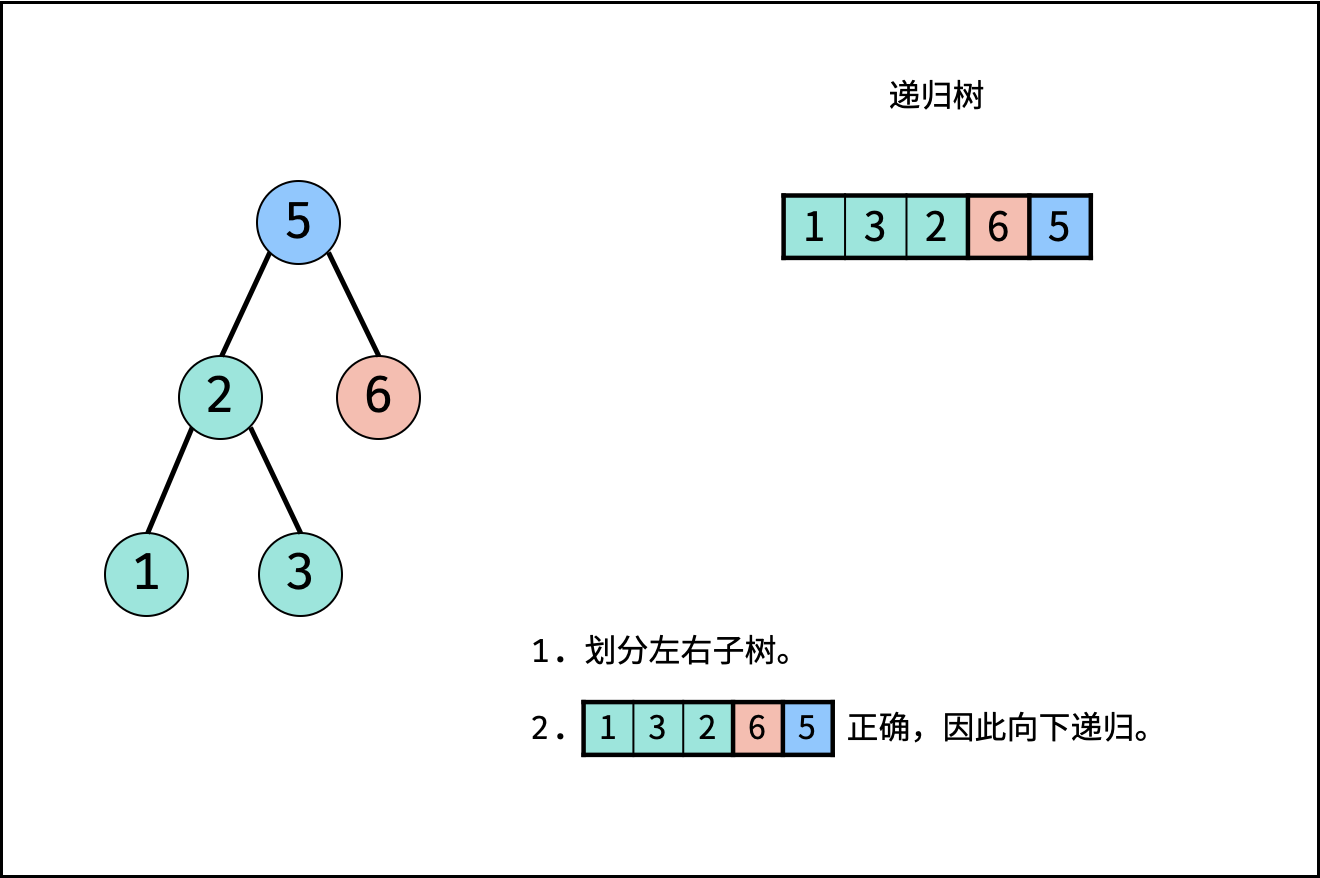
终止条件： 当 $i \geq j$ ，说明此子树节点数量 $\leq 1$ ，无需判别正确性，因此直接返回 $true$ ；
递推工作：
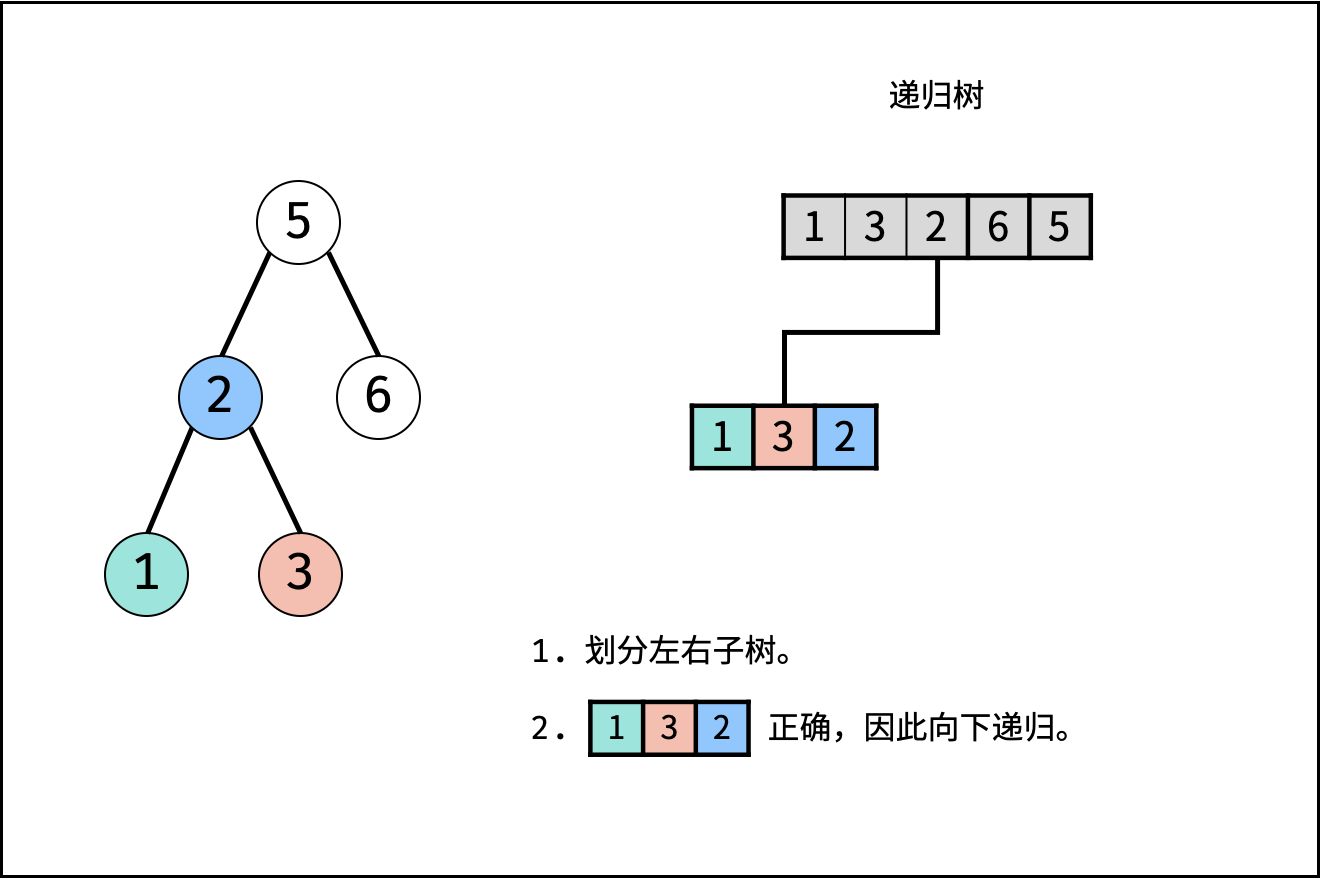
1. 划分左右子树： 遍历后序遍历的 $[i, j]$ 区间元素，寻找 第一个大于根节点 的节点，索引记为 $m$ 。此时，可划分出左子树区间 $[i,m-1]$ 、右子树区间 $[m, j - 1]$ 、根节点索引 $j$ 。
2. 判断是否为二叉搜索树：
  - 左子树区间 $[i, m - 1]$ 内的所有节点都应 $<$ $postorder[j]$ 。而第 1.划分左右子树 步骤已经保证左子树区间的正确性，因此只需要判断右子树区间即可。
  - 右子树区间 $[m, j-1]$ 内的所有节点都应 $>$ $postorder[j]$ 。实现方式为遍历，当遇到 $\leq postorder[j]$ 的节点则跳出；则可通过 $p = j$ 判断是否为二叉搜索树。
返回值： 所有子树都需正确才可判定正确，因此使用 与逻辑符 $&&$ 连接。
1. $p = j$ ： 判断此树是否正确。
2. $recur(i, m - 1)$ ： 判断 此树的左子树 是否正确。
3. $recur(m, j - 1)$ ： 判断 此树的右子树 是否正确。

<,,,,,,,>

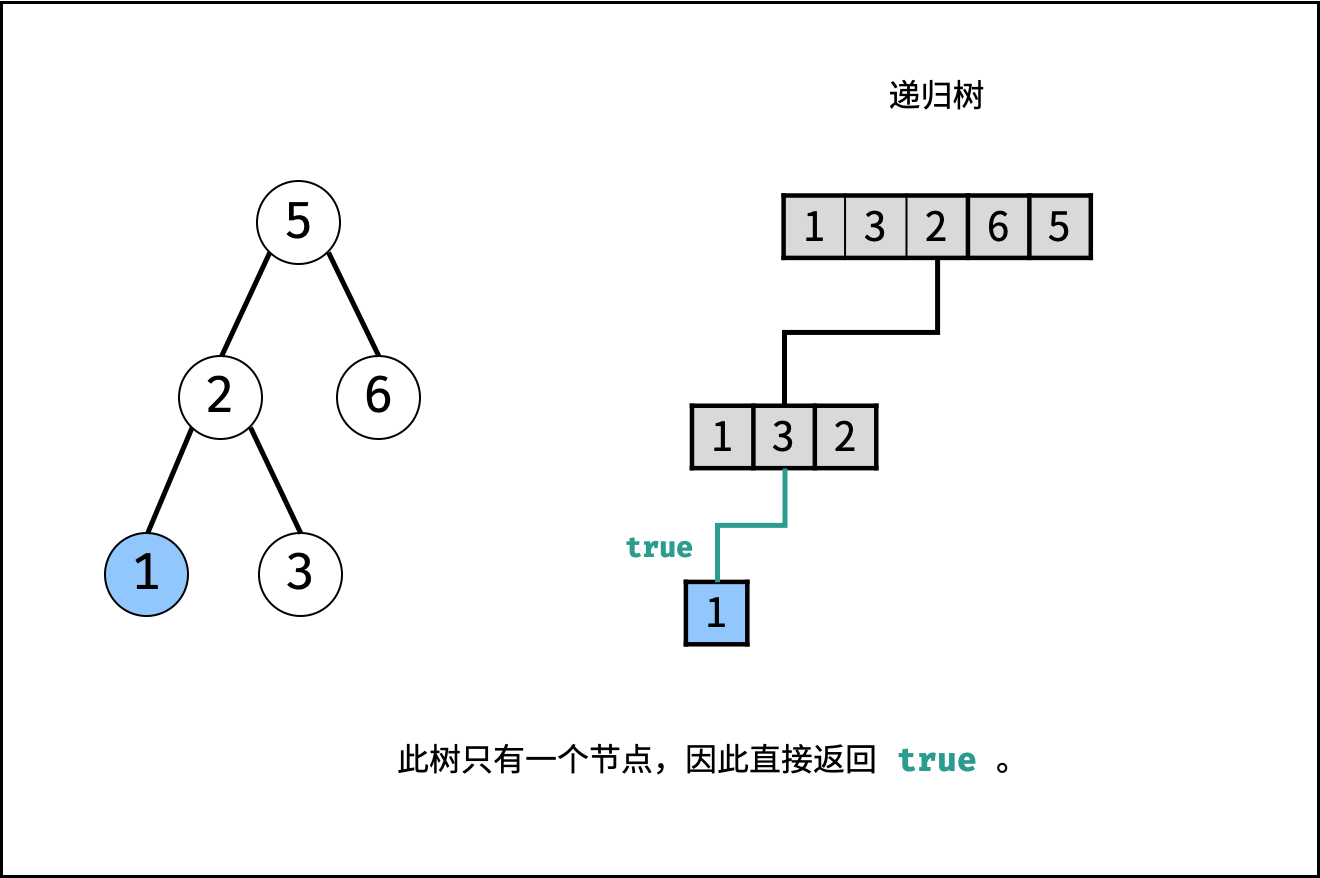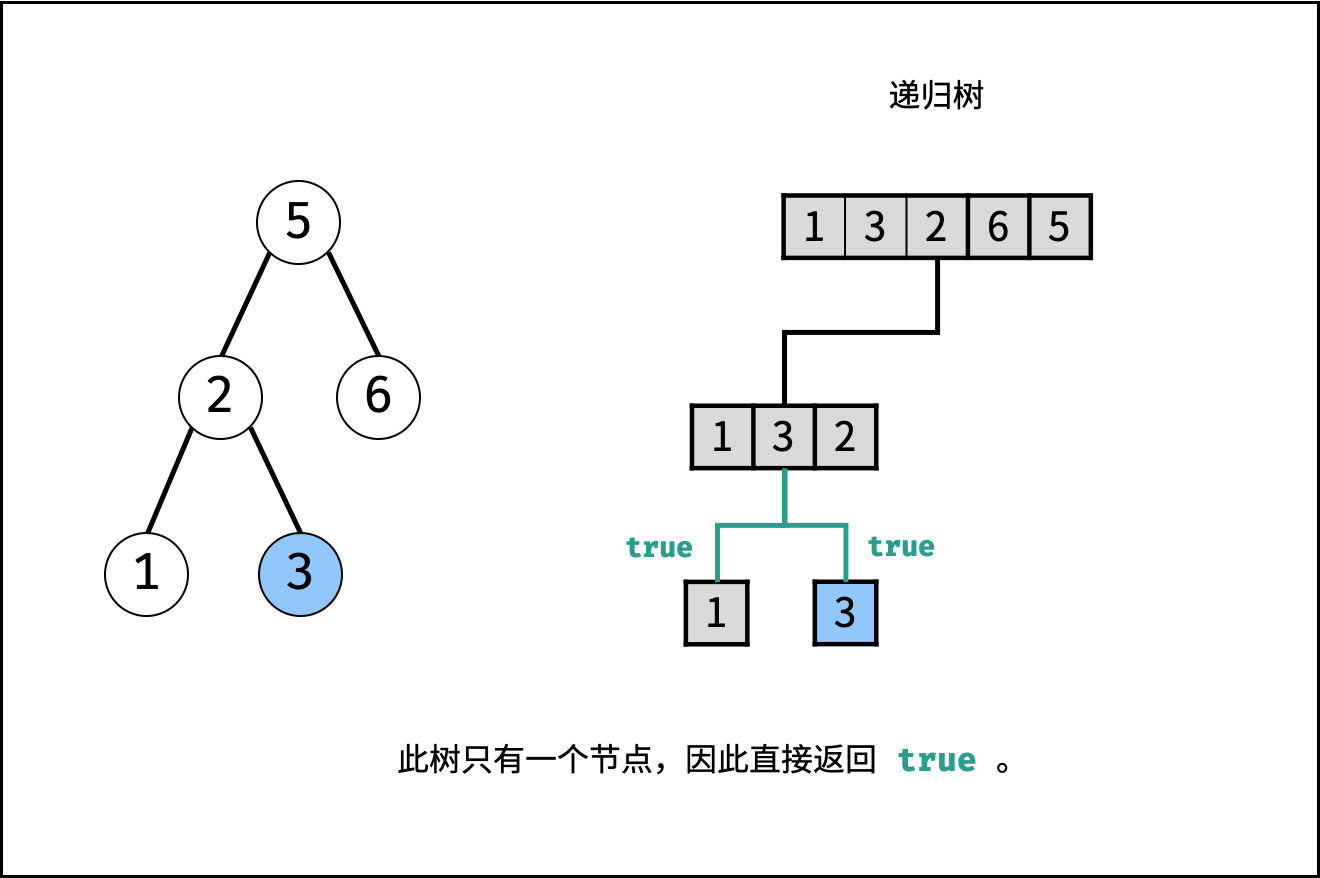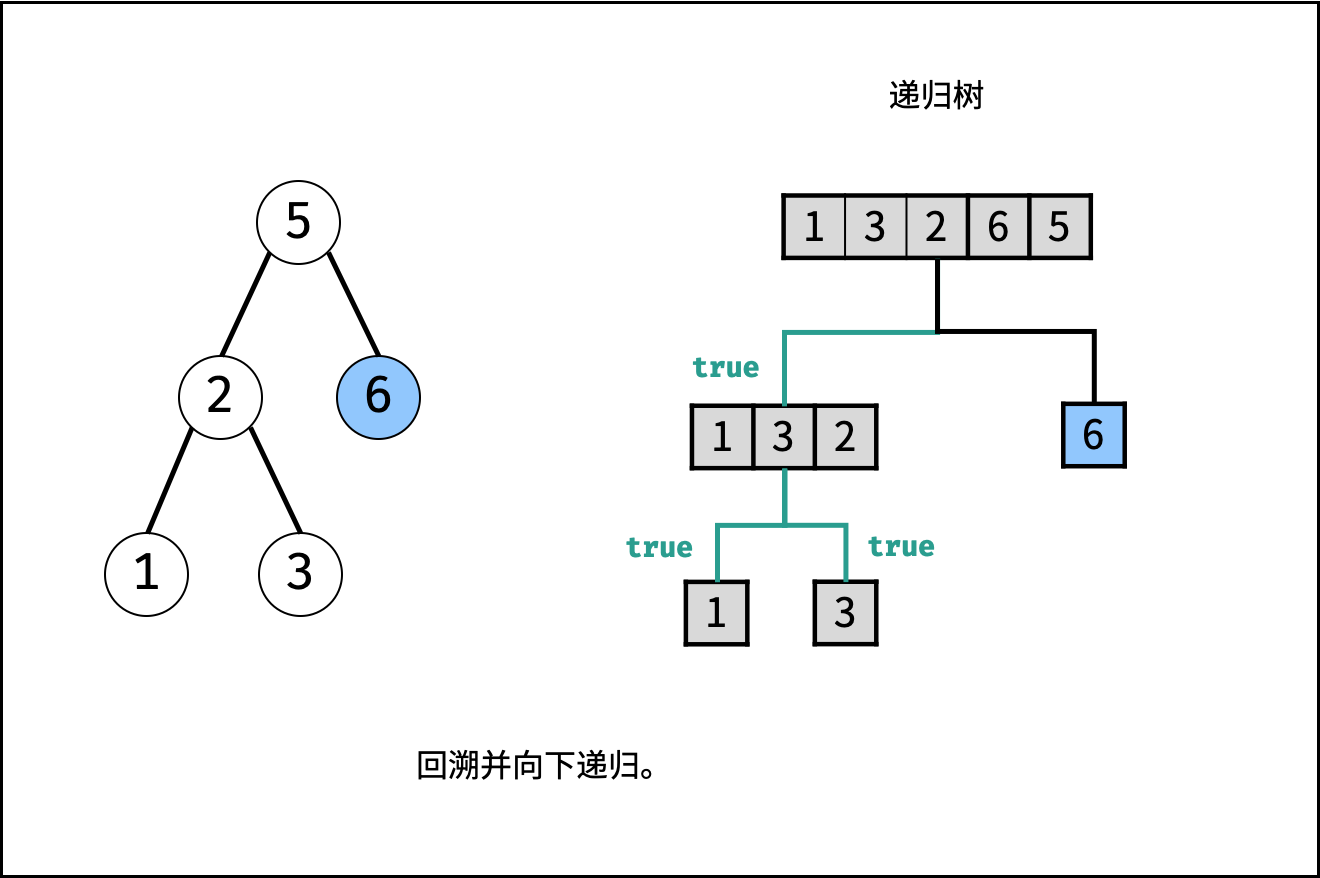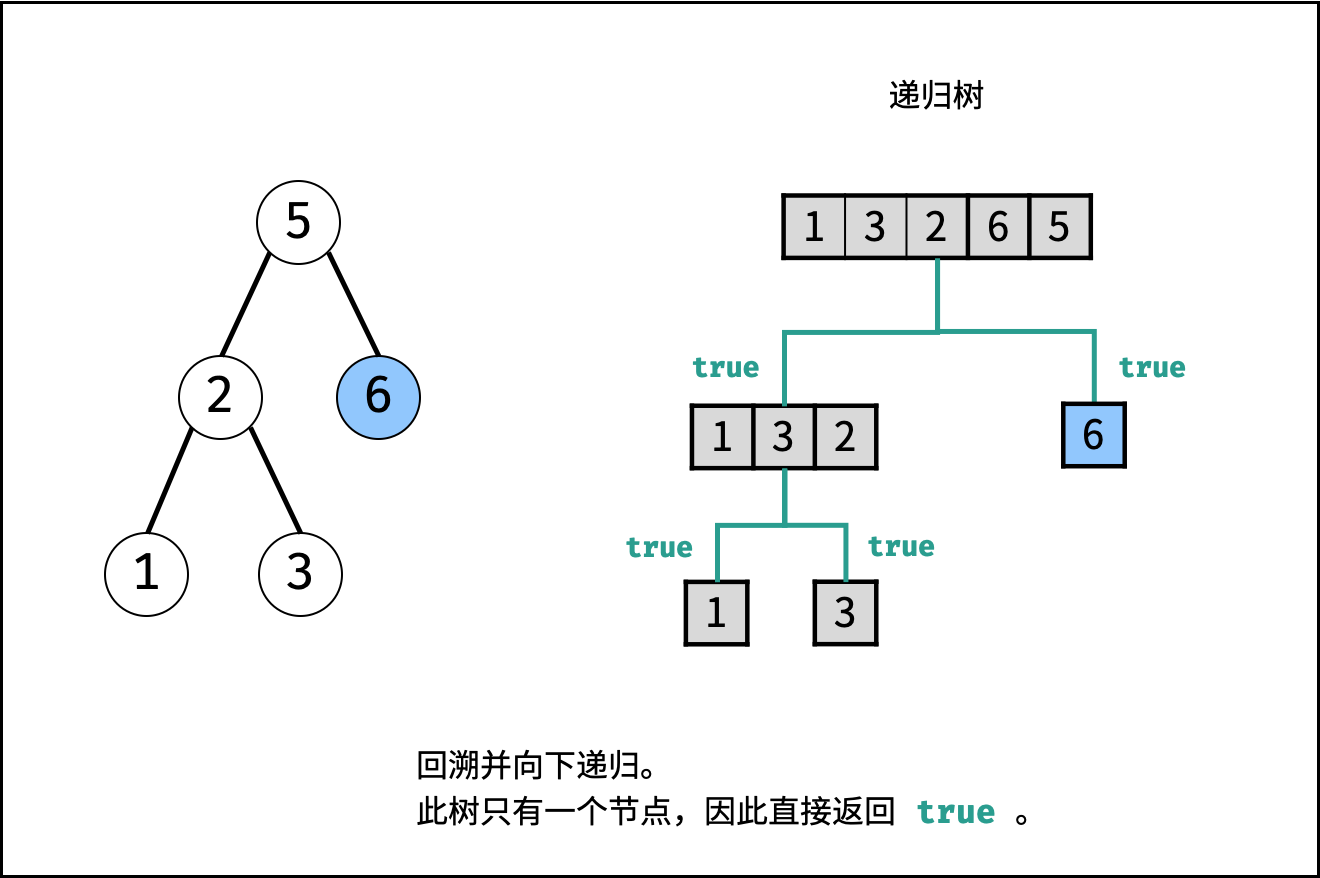复杂度分析：

时间复杂度 $O(N^2)$ ： 每次调用 $recur(i,j)$ 减去一个根节点，因此递归占用 $O(N)$ ；最差情况下（即当树退化为链表），每轮递归都需遍历树所有节点，占用 $O(N)$ 。
空间复杂度 $O(N)$ ： 最差情况下（即当树退化为链表），递归深度将达到 $N$ 。

Python

class Solution:
    def verifyPostorder(self, postorder: [int]) -> bool:
        def recur(i, j):
            if i >= j: return True
            p = i
            while postorder[p] < postorder[j]: p += 1
            m = p
            while postorder[p] > postorder[j]: p += 1
            return p == j and recur(i, m - 1) and recur(m, j - 1)

        return recur(0, len(postorder) - 1)

Java

class Solution {
    public boolean verifyPostorder(int[] postorder) {
        return recur(postorder, 0, postorder.length - 1);
    }
    boolean recur(int[] postorder, int i, int j) {
        if(i >= j) return true;
        int p = i;
        while(postorder[p] < postorder[j]) p++;
        int m = p;
        while(postorder[p] > postorder[j]) p++;
        return p == j && recur(postorder, i, m - 1) && recur(postorder, m, j - 1);
    }
}

C++

class Solution {
public:
    bool verifyPostorder(vector<int>& postorder) {
        return recur(postorder, 0, postorder.size() - 1);
    }
private:
    bool recur(vector<int>& postorder, int i, int j) {
        if(i >= j) return true;
        int p = i;
        while(postorder[p] < postorder[j]) p++;
        int m = p;
        while(postorder[p] > postorder[j]) p++;
        return p == j && recur(postorder, i, m - 1) && recur(postorder, m, j - 1);
    }
};

方法二：辅助单调栈

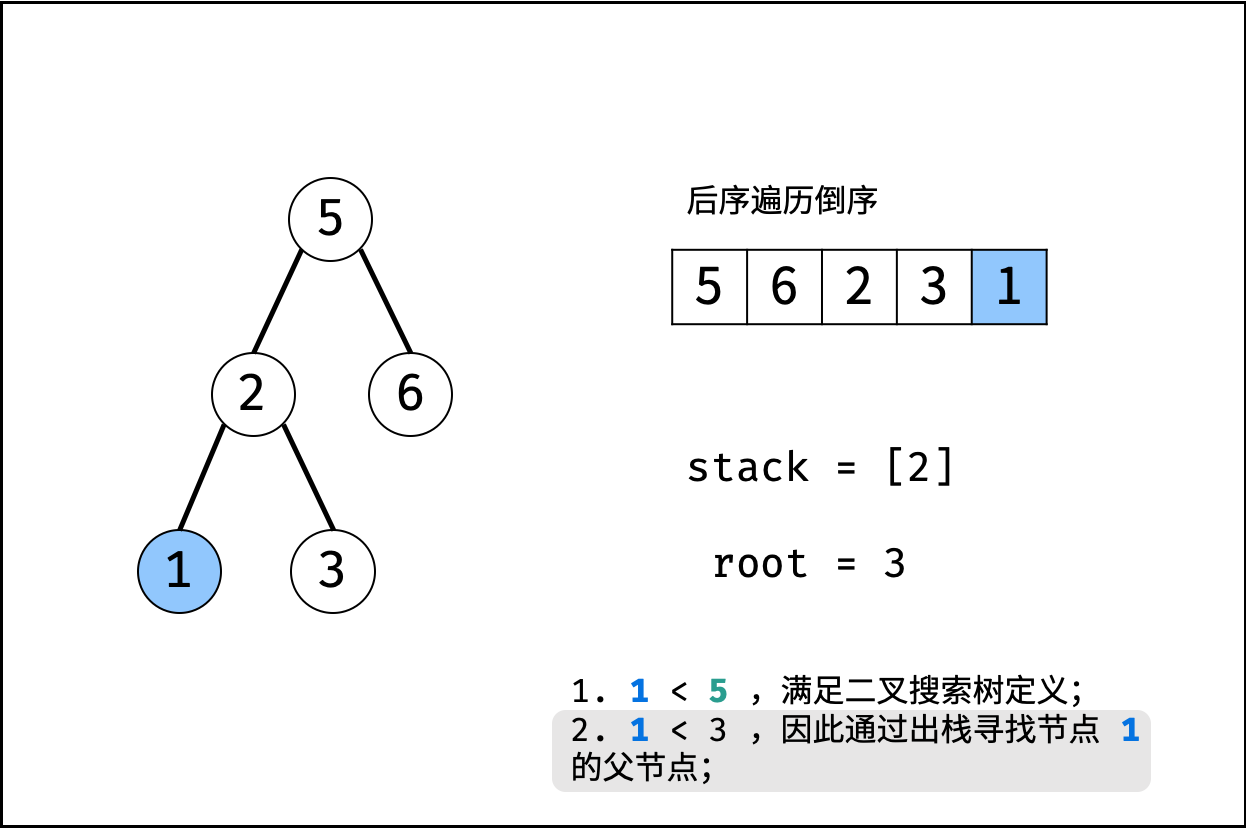
后序遍历倒序： [ 根节点 | 右子树 | 左子树 ] 。类似 先序遍历的镜像 ，即先序遍历为 “根、左、右” 的顺序，而后序遍历的倒序为 “根、右、左” 顺序。

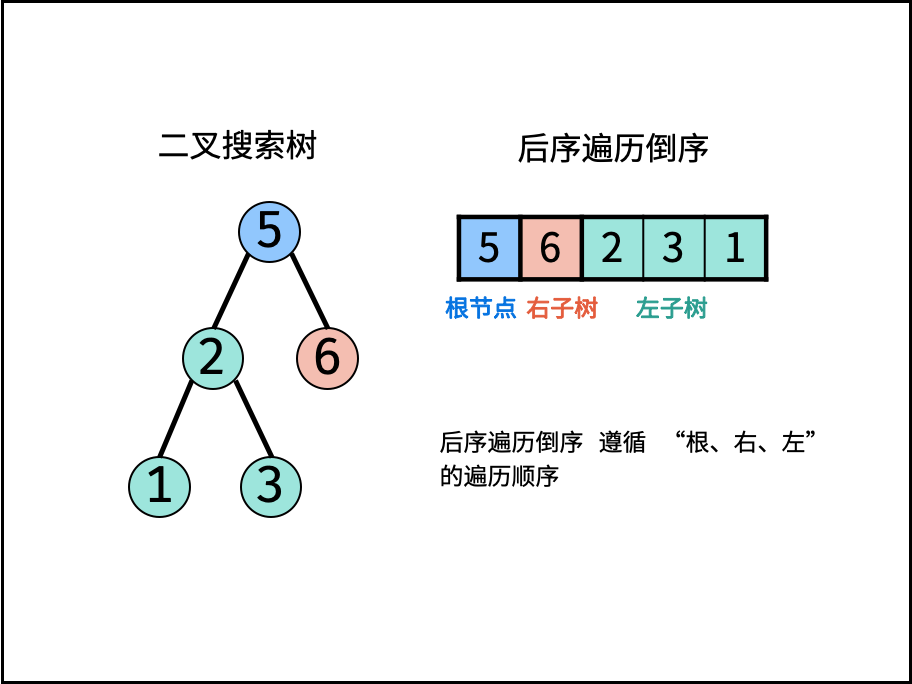
设后序遍历倒序列表为 $[r_{n}, r_{n-1},...,r_1]$，遍历此列表，设索引为 $i$ ，若为 二叉搜索树 ，则有：

当节点值 $r_i > r_{i+1}$ 时： 节点 $r_i$ 一定是节点 $r_{i+1}$ 的右子节点。
当节点值 $r_i < r_{i+1}$ 时： 节点 $r_i$ 一定是某节点 $root$ 的左子节点，且 $root$ 为节点 $r_{i+1}, r_{i+2},..., r_{n}$ 中值大于且最接近 $r_i$ 的节点（∵ $root$ 直接连接 左子节点 $r_i$ ）。

当遍历时遇到递减节点 $r_i < r_{i+1}$ ，若为二叉搜索树，则对于后序遍历中节点 $r_i$ 右边的任意节点 $r_x \in [r_{i-1}, r_{i-2}, ..., r_1]$ ，必有节点值 $r_x < root$ 。

节点 $r_x$ 只可能为以下两种情况：① $r_x$ 为 $r_i$ 的左、右子树的各节点；② $r_x$ 为 $root$ 的父节点或更高层父节点的左子树的各节点。在二叉搜索树中，以上节点都应小于 $root$ 。

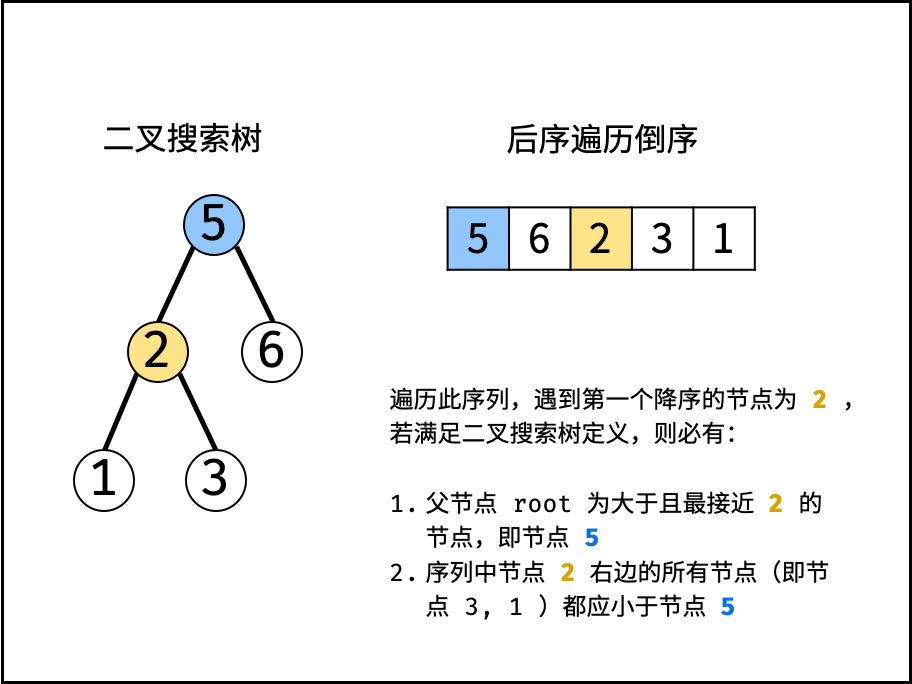
遍历 “后序遍历的倒序” 会多次遇到递减节点 $r_i$ ，若所有的递减节点 $r_i$ 对应的父节点 $root$ 都满足以上条件，则可判定为二叉搜索树。根据以上特点，考虑借助 单调栈 实现：

借助一个单调栈 $stack$ 存储值递增的节点；
每当遇到值递减的节点 $r_i$ ，则通过出栈来更新节点 $r_i$ 的父节点 $root$ ；
每轮判断 $r_i$ 和 $root$ 的值关系：
1. 若 $r_i > root$ 则说明不满足二叉搜索树定义，直接返回 $false$ 。
2. 若 $r_i < root$ 则说明满足二叉搜索树定义，则继续遍历。

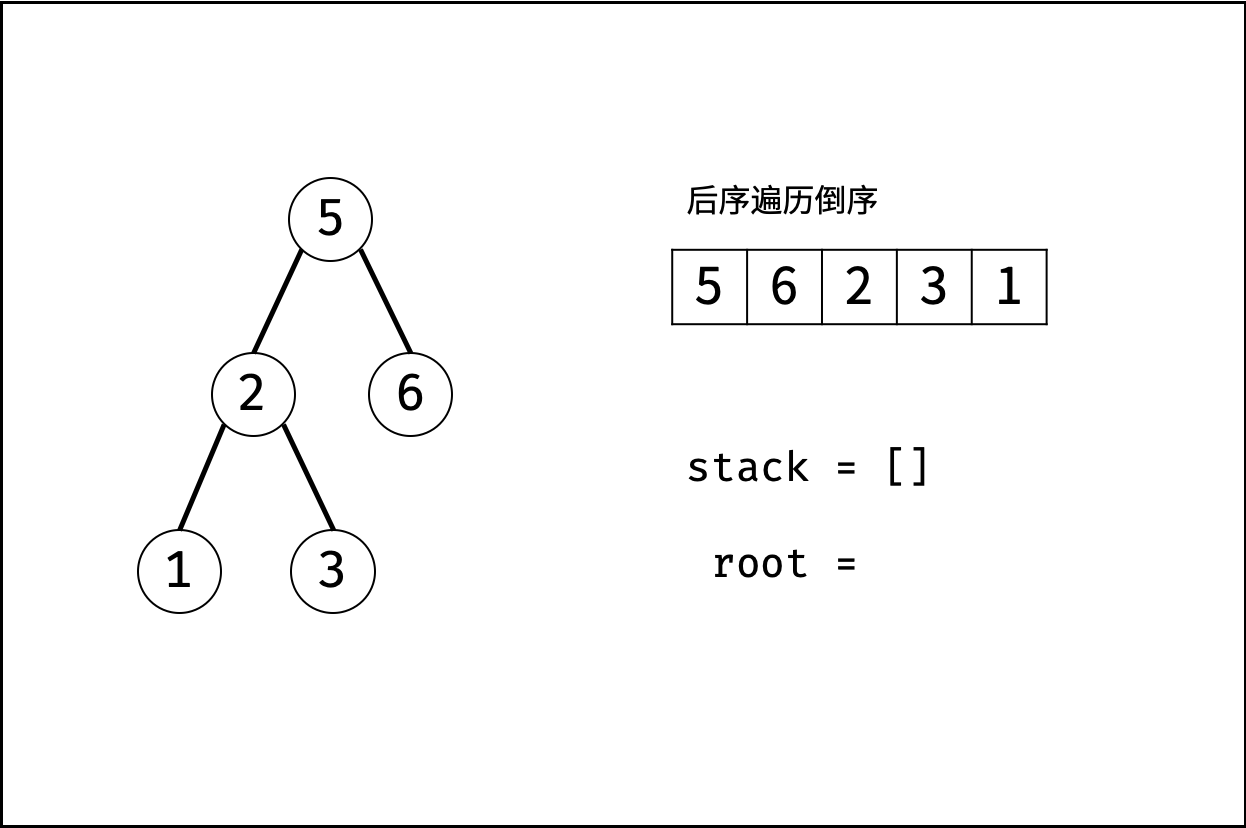
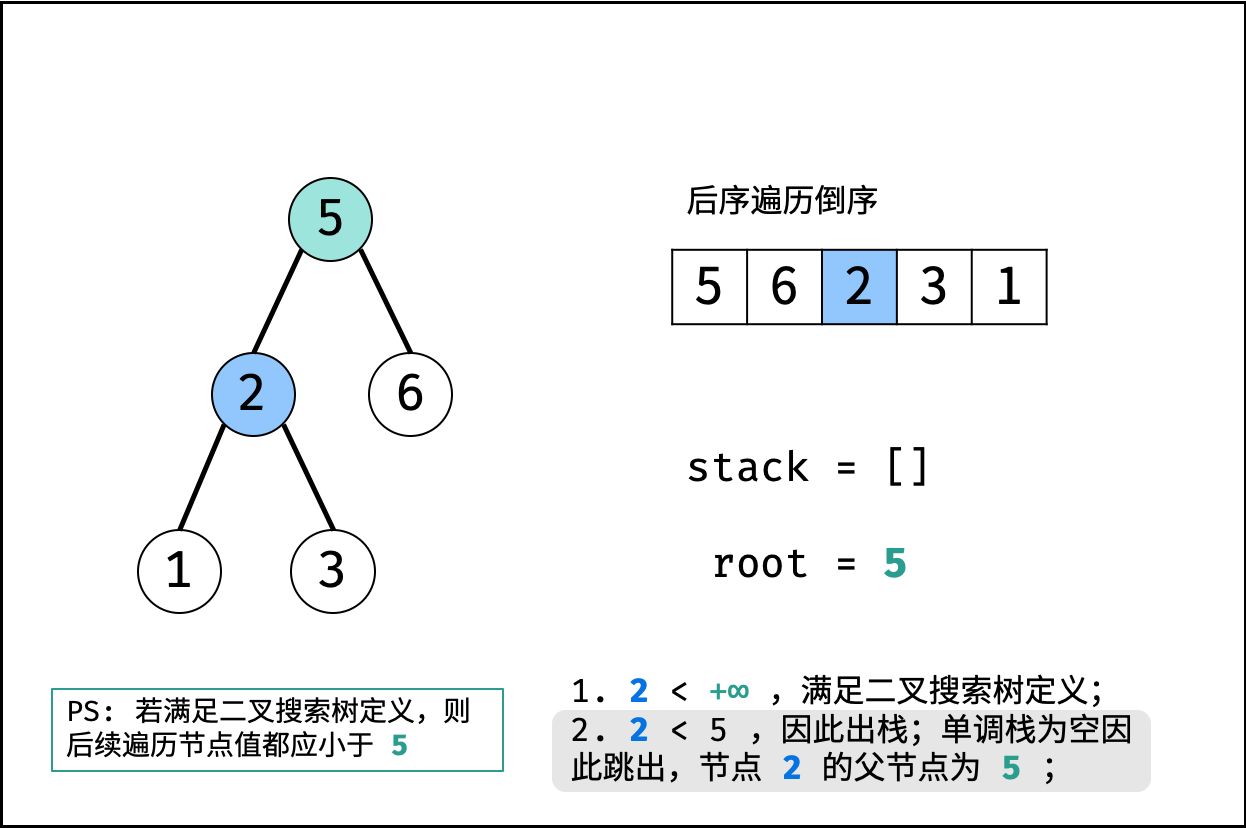
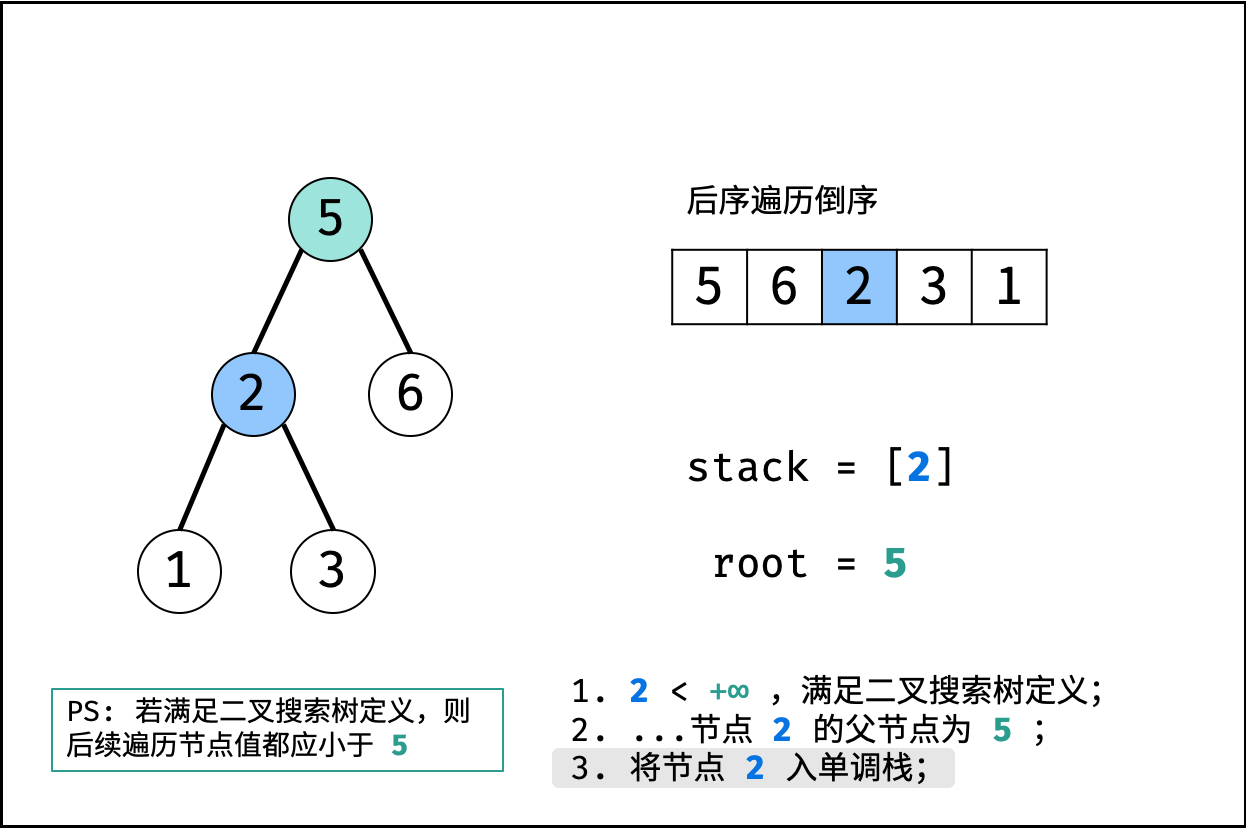
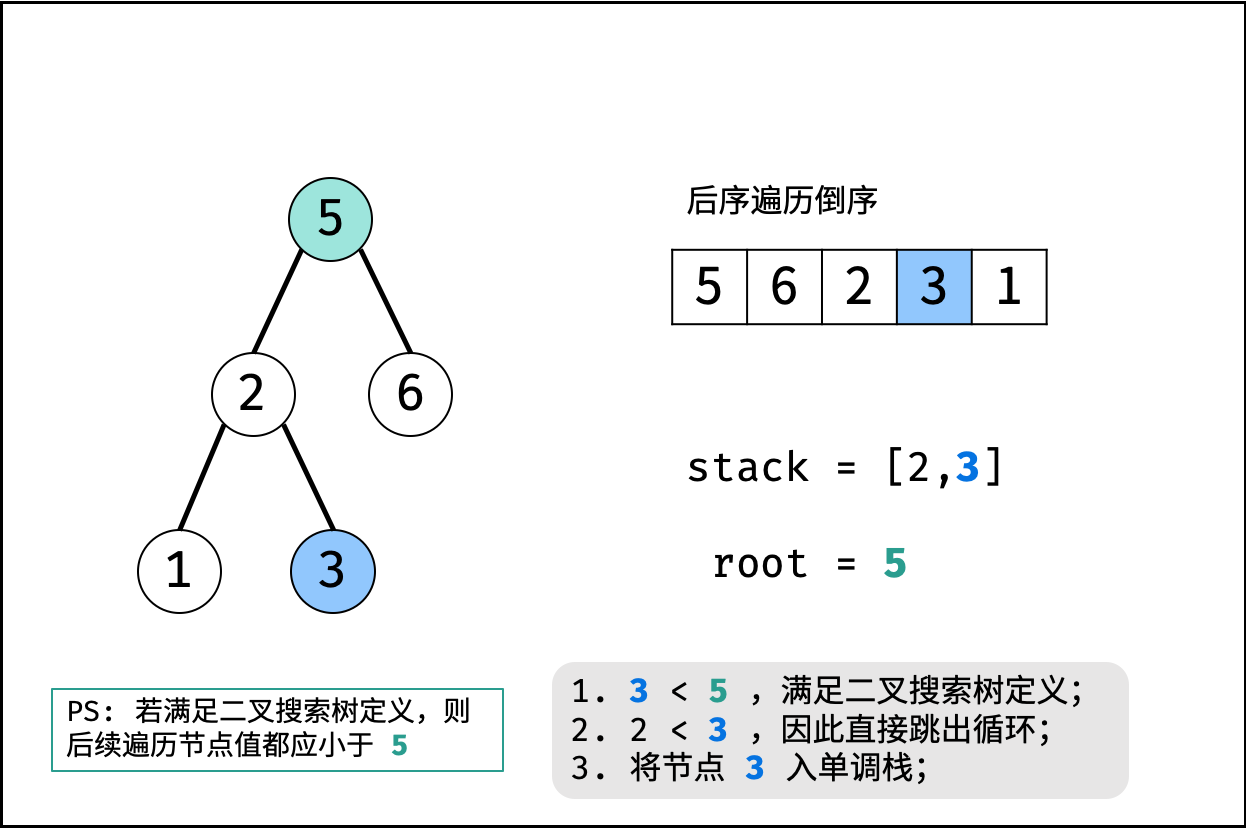
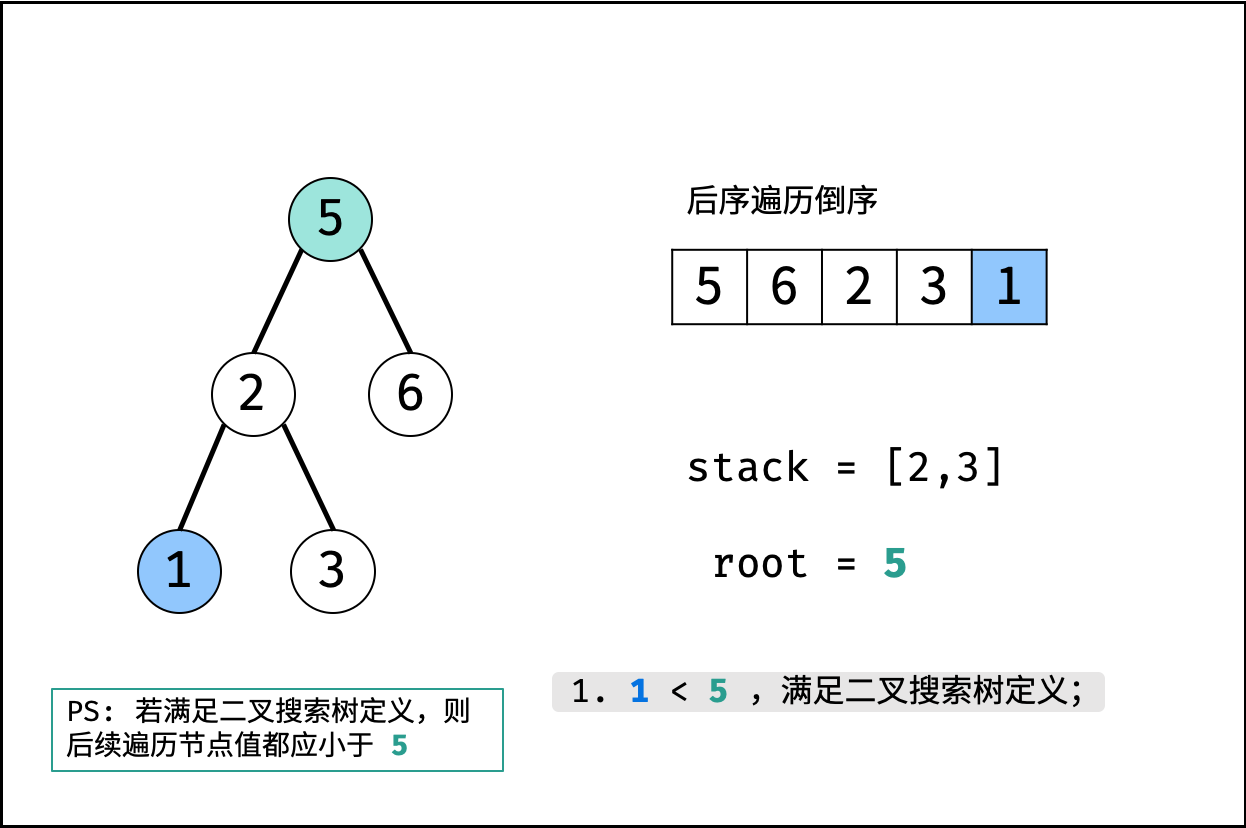
算法流程：

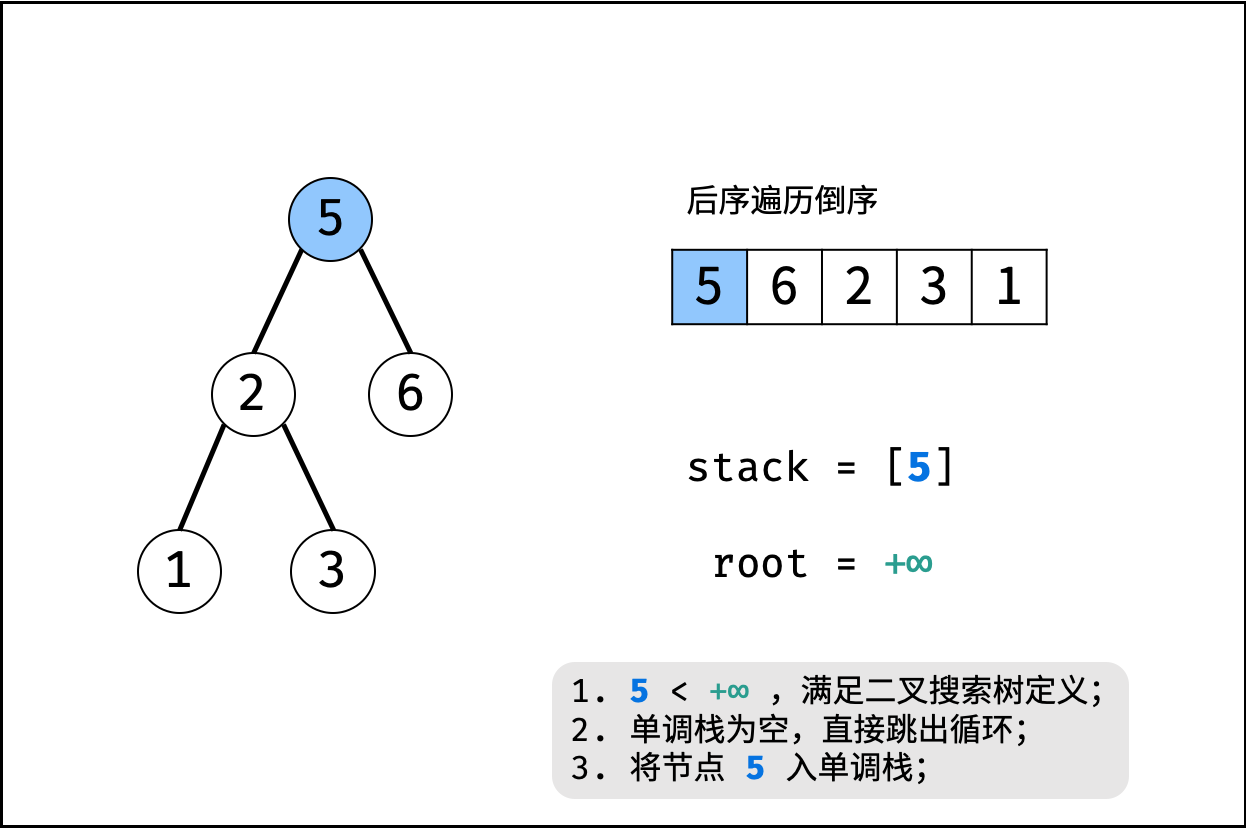
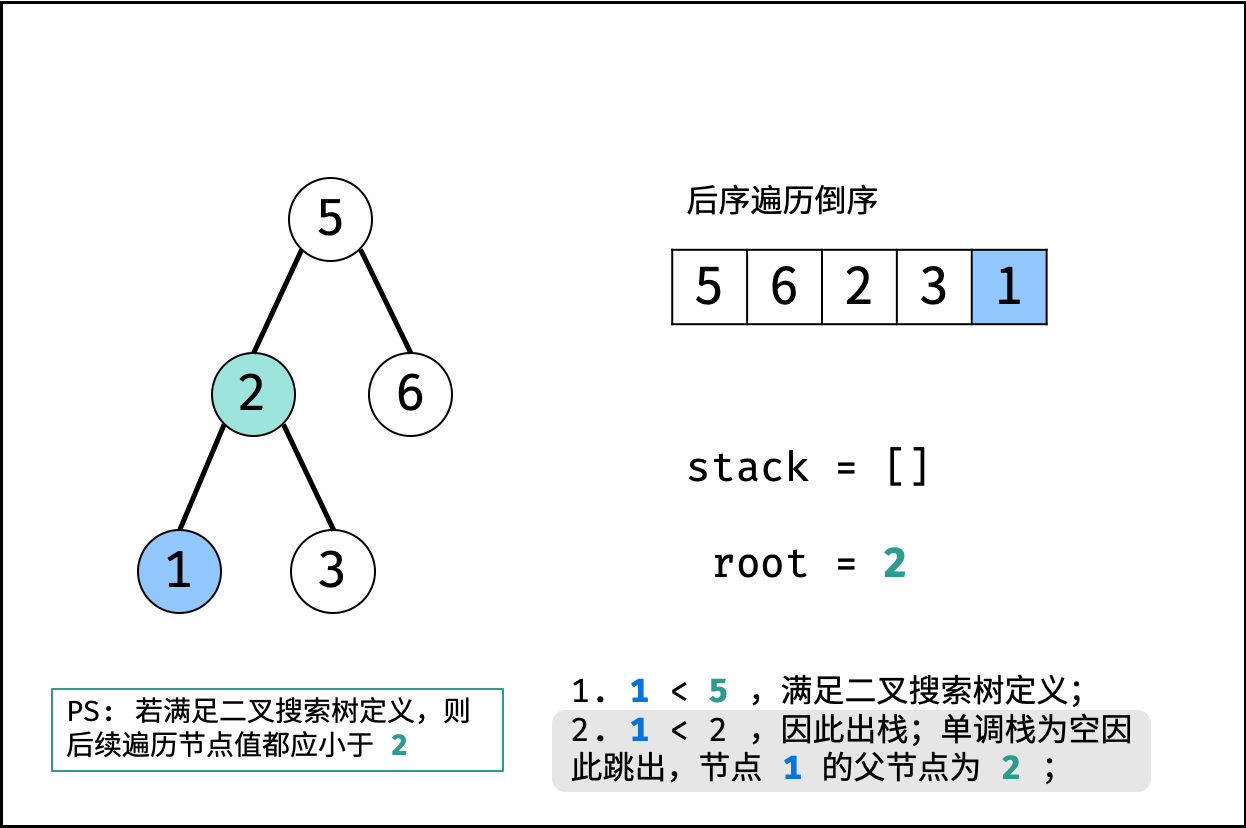
初始化： 单调栈 $stack$ ，父节点值 $root = +\infin$ （初始值为正无穷大，可把树的根节点看为此无穷大节点的左孩子）；
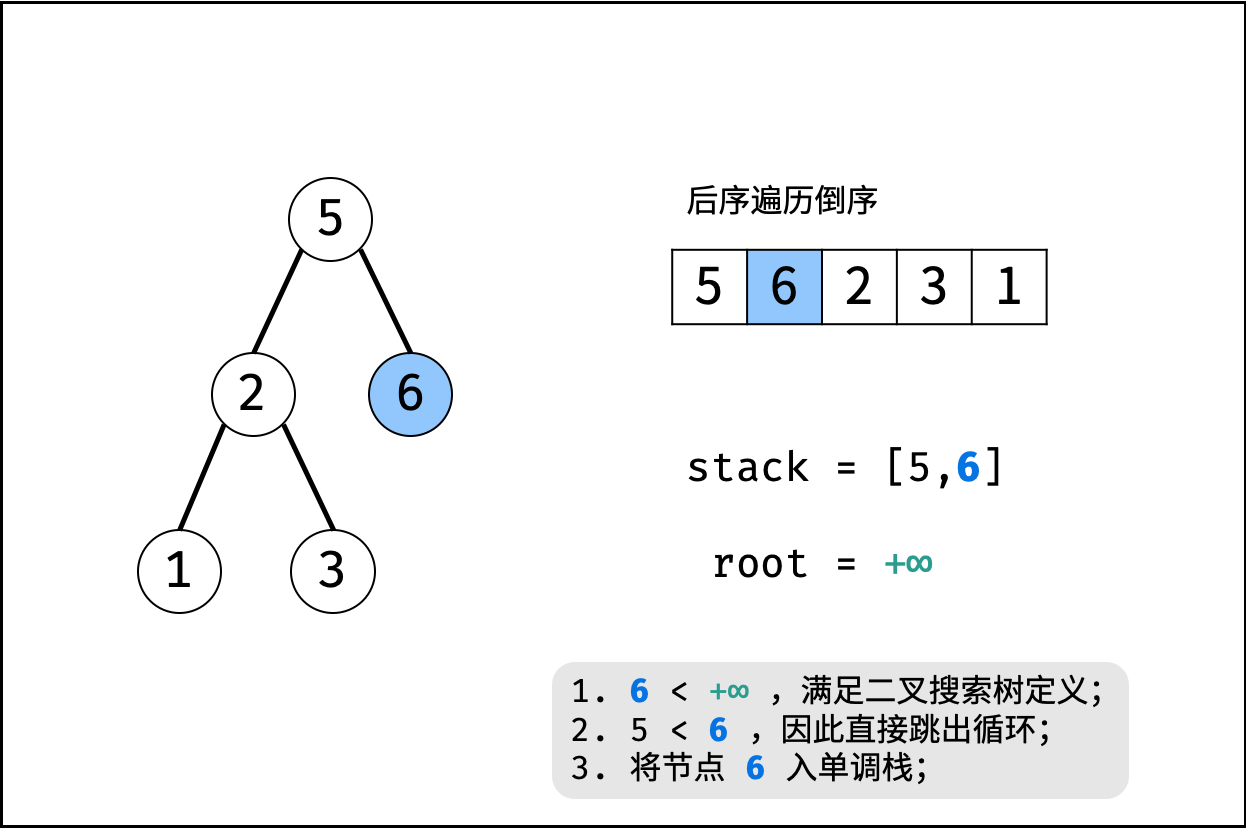
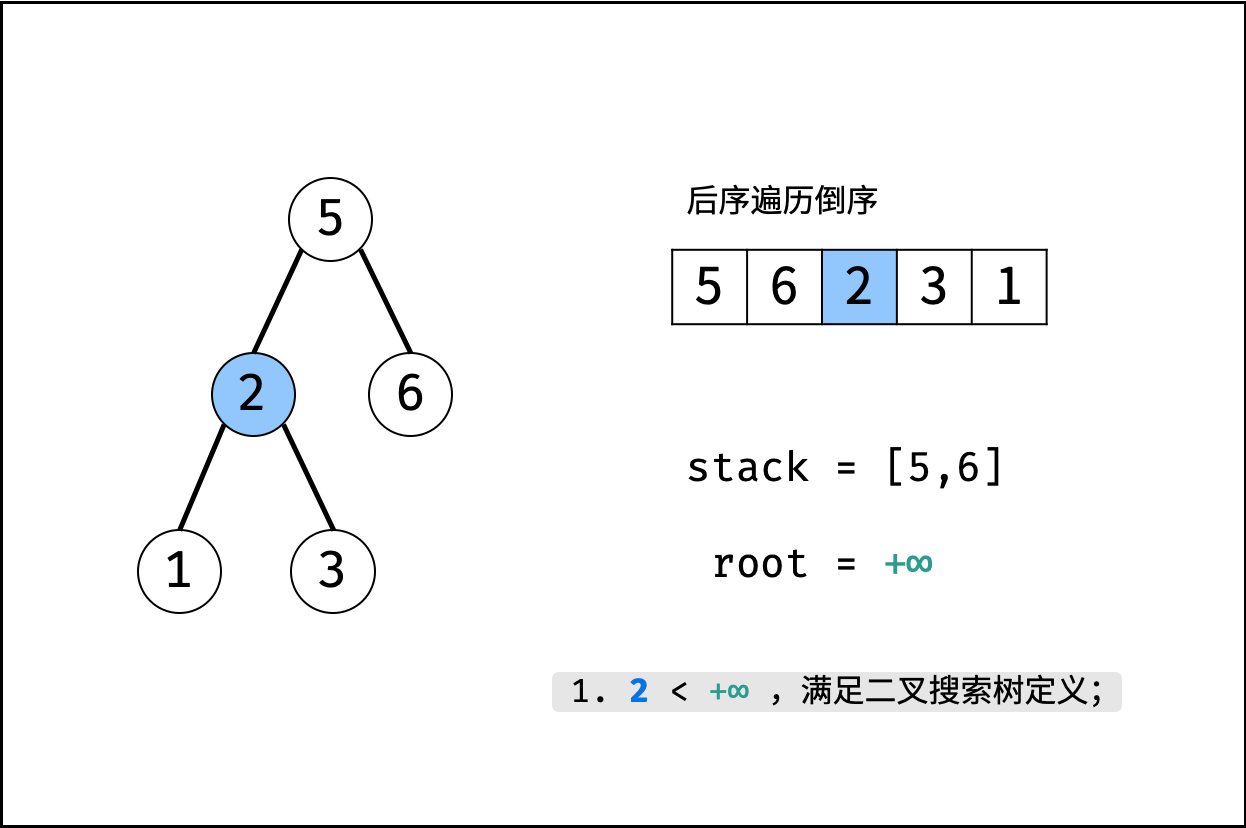
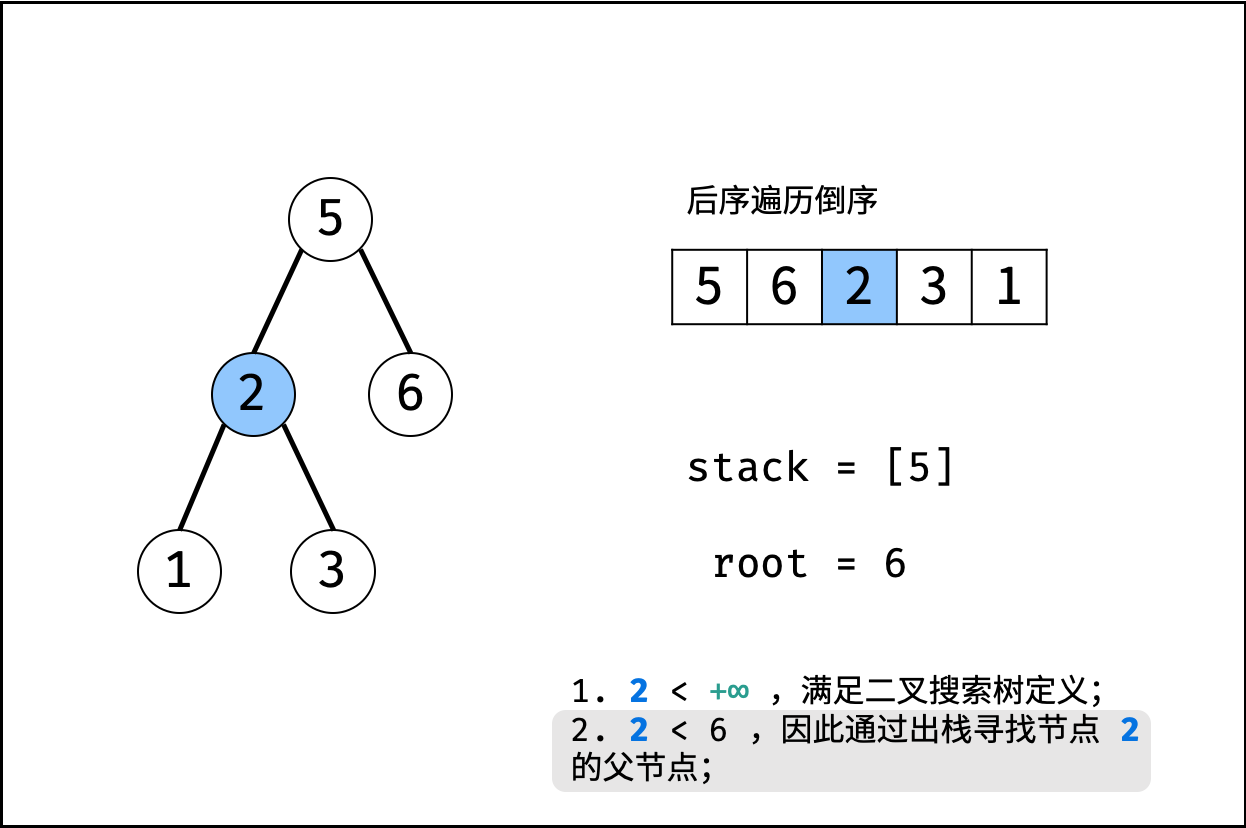
倒序遍历 $postorder$ ：记每个节点为 $r_i$；
1. 判断： 若 $r_i>root$ ，说明此后序遍历序列不满足二叉搜索树定义，直接返回 $false$ ；
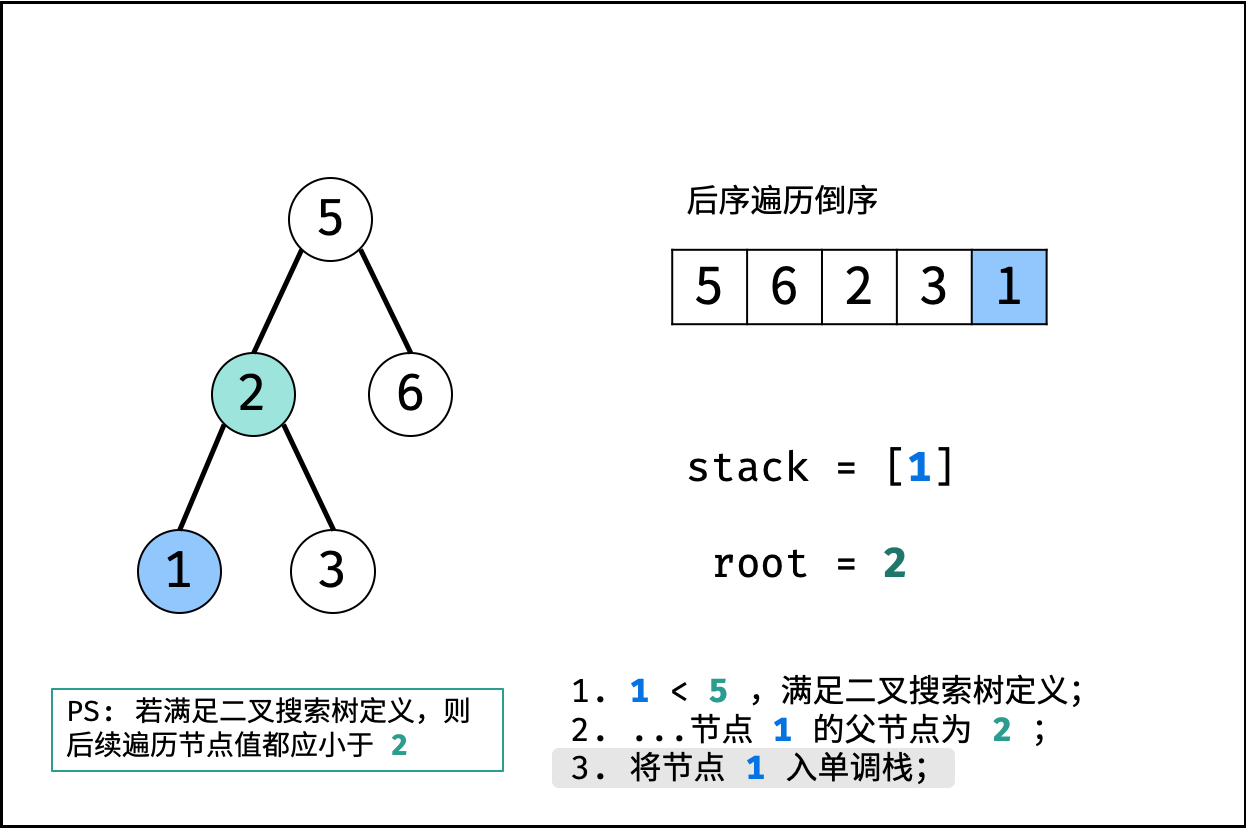
2. 更新父节点 $root$ ： 当栈不为空且 $r_i<stack.peek()$ 时，循环执行出栈，并将出栈节点赋给 $root$ 。
3. 入栈： 将当前节点 $r_i$ 入栈；
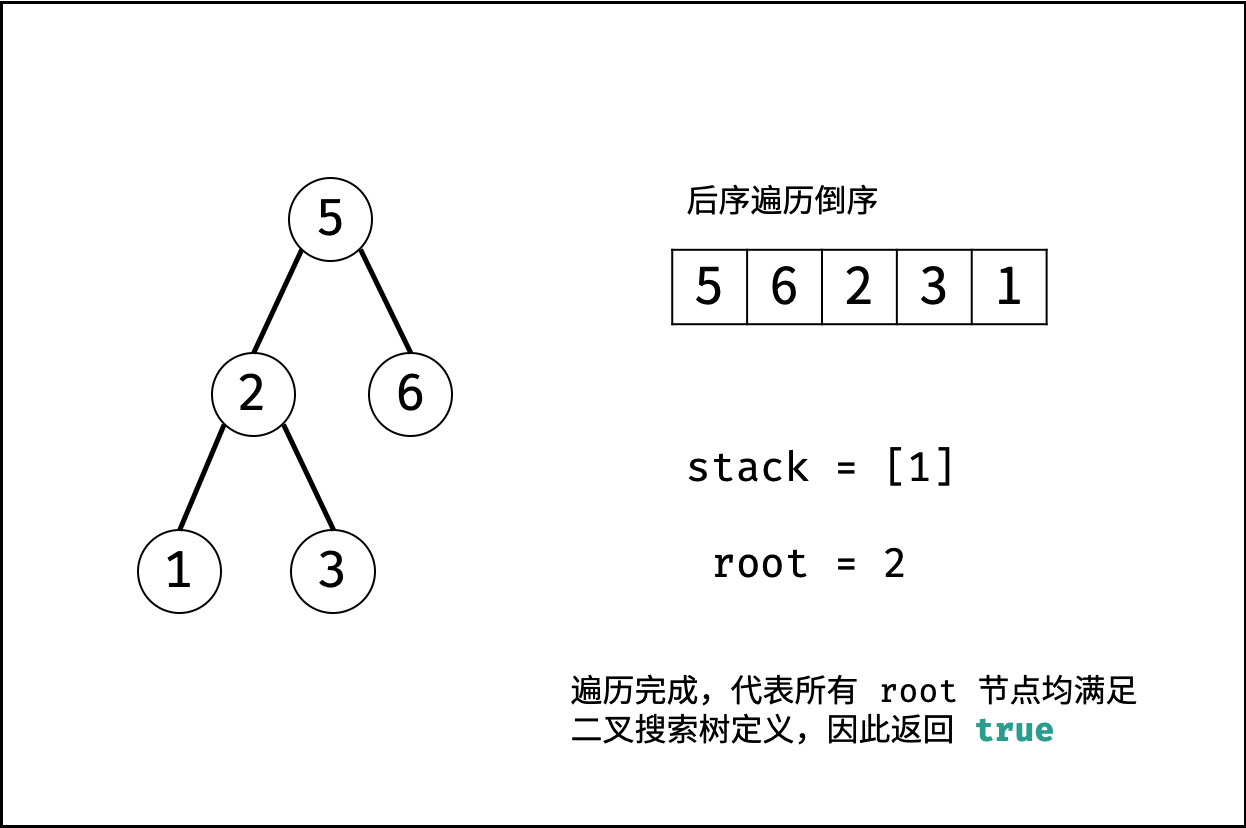
若遍历完成，则说明后序遍历满足二叉搜索树定义，返回 $true$ 。

<,,,,,,,,,,,,>

复杂度分析：

时间复杂度 $O(N)$ ： 遍历 $postorder$ 所有节点，各节点均入栈 / 出栈一次，使用 $O(N)$ 时间。
空间复杂度 $O(N)$ ： 最差情况下，单调栈 $stack$ 存储所有节点，使用 $O(N)$ 额外空间。

Python

class Solution:
    def verifyPostorder(self, postorder: [int]) -> bool:
        stack, root = [], float("+inf")
        for i in range(len(postorder) - 1, -1, -1):
            if postorder[i] > root: return False
            while(stack and postorder[i] < stack[-1]):
                root = stack.pop()
            stack.append(postorder[i])
        return True

Java

class Solution {
    public boolean verifyPostorder(int[] postorder) {
        Stack<Integer> stack = new Stack<>();
        int root = Integer.MAX_VALUE;
        for(int i = postorder.length - 1; i >= 0; i--) {
            if(postorder[i] > root) return false;
            while(!stack.isEmpty() && stack.peek() > postorder[i])
                root = stack.pop();
            stack.add(postorder[i]);
        }
        return true;
    }
}

C++

class Solution {
public:
    bool verifyPostorder(vector<int>& postorder) {
        stack<int> stk;
        int root = INT_MAX;
        for(int i = postorder.size() - 1; i >= 0; i--) {
            if(postorder[i] > root) return false;
            while(!stk.empty() && stk.top() > postorder[i]) {
                root = stk.top();
                stk.pop();
            }
            stk.push(postorder[i]);
        }
        return true;
    }
};

解题思路： ​

方法一：递归分治 ​

递归解析： ​

方法二：辅助单调栈 ​

算法流程： ​

解题思路：

方法一：递归分治

递归解析：

方法二：辅助单调栈

算法流程：